In diesem Artikel verrate ich euch schnell und einfach die Grundlagen zum Ableiten von Funktionen. Mit einem kurzen Überblick über wichtige Ableitungsregeln und praktischen Tipps werdet ihr im Handumdrehen zum Ableitungsprofi. Um das Ganze anschaulich zu machen, verwende ich Bilder und ein aufschlussreiches Video.
Überblick wichtiger Ableitungsregeln
Um erfolgreich Ableitungen durchzuführen, ist es wichtig, die grundlegenden Ableitungsregeln zu kennen. In diesem Bild findet ihr einen übersichtlichen Überblick über diese Regeln.
Warum bilden wir eine Ableitung?
Ableitungen spielen eine entscheidende Rolle bei der Kurvendiskussion von Funktionen. Durch die Ableitung können wir unter anderem Extremwerte bestimmen und erkennen, ob es sich um einen Hoch- oder Tiefpunkt handelt. Die Ableitung gibt uns also wichtige Informationen über das Verhalten der Funktion.
Grundlagen zum Ableiten
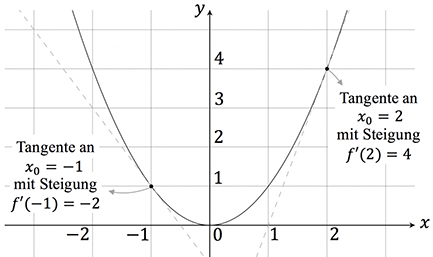
Das Ableiten einer Funktion ist geometrisch gesehen gleichbedeutend mit der Bestimmung der Tangentensteigung an einem bestimmten Punkt. Stellt euch vor, ihr habt eine Funktion wie z.B. f(x) = x^2. Die Ableitung dieser Funktion, f'(x) = 2x, gibt euch die Steigung der Tangente an jedem Punkt x.
Anhand dieser Abbildung könnt ihr sehen, wie die Ableitung mit der Tangentensteigung zusammenhängt. Wenn ihr bestimmte Werte für x einsetzt, erhaltet ihr die entsprechende Tangentensteigung. Liegt x in einem Bereich, in dem die Kurve steigt, ist die Ableitung f'(x) > 0. Liegt x in einem Bereich, in dem die Kurve fällt, ist f'(x) < 0.
Grafisches Ableiten und Aufleiten
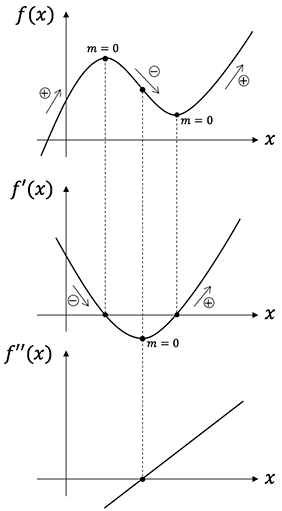
Die Beziehung zwischen der Funktion f(x), ihrer Ableitung f'(x) und der zweiten Ableitung f”(x) wird in der folgenden Grafik veranschaulicht. N steht hierbei für die Nullstelle, E für den Extrempunkt und W für den Wendepunkt.
f(x) N E W f'(x) N E W f''(x) N E WDiese Tabelle zeigt, welche Funktion uns welche Informationen zur Ableitung oder Aufleitung liefert. Anhand der Abbildung könnt ihr die Zusammenhänge noch genauer verstehen.
Kettenregel
Die Kettenregel wird angewendet, wenn wir eine Verkettung von Funktionen haben. Dabei gibt es eine äußere Funktion und eine innere Funktion. Die Kettenregel besagt, dass die Ableitung einer Verkettung einer Funktion die Ableitung der inneren Funktion multipliziert mit der Ableitung der äußeren Funktion ist. Um dies besser zu verstehen, betrachten wir ein einfaches Beispiel:
f(x) = (x^3 + 2)^2Hier haben wir eine äußere Funktion g(h) = h^2 und eine innere Funktion h(x) = x^3 + 2. Die Ableitung dieser Funktion ergibt sich mit Hilfe der Kettenregel:
f'(x) = h'(x) * g'(h(x))Angewendet auf unser Beispiel erhalten wir:
f'(x) = 3x^2 * 2 * (x^3 + 2)Diese Regel kann auch auf kompliziertere Potenzausdrücke angewendet werden:
(d/(dx))((etwas)^p) = p * (etwas)^(p-1) * (etwas)'Produktregel
Die Produktregel wird angewendet, wenn wir eine Funktion haben, die aus zwei miteinander multiplizierten Faktoren besteht. Die Produktregel besagt, dass die Ableitung eines Produkts zweier Funktionen gleich der Ableitung der ersten Funktion multipliziert mit der zweiten Funktion plus der ersten Funktion multipliziert mit der Ableitung der zweiten Funktion ist. Betrachten wir ein Beispiel:
f(x) = 2x * e^xHier haben wir die beiden Faktoren 2x und e^x. Die Ableitung ergibt sich mit Hilfe der Produktregel:
f'(x) = u'(x) * v(x) + u(x) * v'(x)Angewendet auf unser Beispiel erhalten wir:
f'(x) = 2 * e^x + 2x * e^xQuotientenregel
Die Quotientenregel wird angewendet, wenn wir eine Funktion haben, die als Bruch dargestellt ist. Die Quotientenregel besagt, dass die Ableitung eines Quotients gleich dem Zähler mal der Ableitung des Nenners minus dem Nenner mal der Ableitung des Zählers geteilt durch den Nenner zum Quadrat ist. Betrachten wir ein Beispiel:
f(x) = (x^3 + 2) / x^5Hier haben wir den Zähler u(x) = x^3 + 2 und den Nenner v(x) = x^5. Die Ableitung ergibt sich mit Hilfe der Quotientenregel:
f'(x) = (u'(x) * v(x) - u(x) * v'(x)) / v(x)^2Angewendet auf unser Beispiel erhalten wir:
f'(x) = (-2x^7 - 10x^4) / x^10Ableitungsregeln
Um Funktionen korrekt ableiten zu können, ist es wichtig, die grundlegenden Ableitungsregeln zu kennen. Hier sind einige davon:
- Ableiten einer Konstanten:
f(x) = C => f'(x) = 0 - Ableiten von x:
f(x) = x => f'(x) = 1 - Potenzregel:
f(x) = x^p => f'(x) = p * x^(p-1) - Faktorregel:
f(x) = c * g(x) => f'(x) = c * g'(x) - Summen-/Differenzregel:
f(x) = g(x) ± h(x) => f'(x) = g'(x) ± h'(x)
Neben diesen Regeln gibt es noch weitere, insbesondere für e-Funktionen und ln-Funktionen. Die Ableitung der e-Funktion e^x ist ebenfalls e^x. Für eine vertiefende Erklärung und weitere Beispiele schaut euch das Lernvideo an.
e- und ln-Funktion ableiten
Die Ableitung einer e-Funktion ist sehr einfach. Nehmen wir die Funktion f(x) = e^(5x) als Beispiel. Die Ableitung ergibt sich durch Multiplikation des Terms mit dem abgeleiteten Exponenten:
f'(x) = e^(5x) * 5Diese Regel lässt sich verallgemeinern:
(d/(dx))(e^(etwas)) = e^(etwas) * (etwas)'Für ln-Funktionen gibt es ebenfalls eine einfache Ableitungsregel:
(d/(dx))(ln(x)) = 1/xWeitere Ableitungsregeln für e-Funktionen und ln-Funktionen findet ihr in der Tabelle im Artikel.
Jetzt seid ihr bestens vorbereitet, um Funktionen zu ableiten. Mit den Grundlagen und Regeln könnt ihr problemlos Ableitungen berechnen und euch in der Welt der Ableitungen sicher bewegen. Viel Spaß beim Ausprobieren und Entdecken!