Das Baumdiagramm ist ein nützliches Werkzeug zur Berechnung von Wahrscheinlichkeiten bei mehrstufigen Zufallsexperimenten. In diesem Artikel werden wir verschiedene Aspekte von Baumdiagrammen behandeln und einige praktische Anwendungen betrachten.
Mit oder ohne Zurücklegen?
Die grundlegende Frage, die wir uns stellen müssen, ist, ob das Zufallsexperiment mit oder ohne Zurücklegen durchgeführt wird. Um den Unterschied zu verdeutlichen, betrachten wir ein Beispiel:
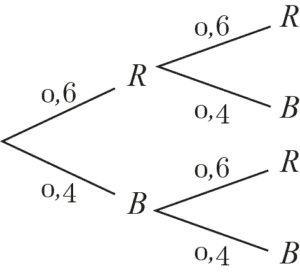
In einer Urne befinden sich 60 rote und 40 blaue Kugeln. Wir ziehen zwei Kugeln mit Zurücklegen.
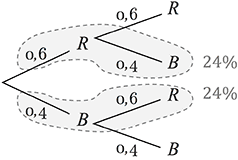
In diesem Szenario können wir die Laplace-Wahrscheinlichkeit anwenden, da alle Ereignisse die gleiche Wahrscheinlichkeit haben. Die Wahrscheinlichkeiten für das Ziehen einer roten oder blauen Kugel betragen jeweils 0,6 bzw. 0,4.
Zufallsexperiment “Ohne Zurücklegen”
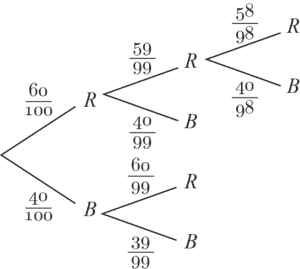
Nun betrachten wir das gleiche Zufallsexperiment, jedoch ohne Zurücklegen.
Im Gegensatz zum Ziehen mit Zurücklegen ändern sich die Wahrscheinlichkeiten beim Ziehen ohne Zurücklegen im zweiten Zug. Die Anzahl der günstigen und der möglichen Ereignisse verringert sich um 1, da eine rote Kugel bereits gezogen wurde. Daher verwenden wir hier Brüche statt Dezimalzahlen für die Wahrscheinlichkeiten.
Wahrscheinlichkeit mit Pfadregel
Die Pfadregel ist eine wichtige Methode zur Berechnung von Wahrscheinlichkeiten bei mehrstufigen Zufallsexperimenten.
Um die Wahrscheinlichkeit eines Ergebnisses zu bestimmen, multiplizieren wir die Wahrscheinlichkeiten entlang des Pfades, der zu diesem Ergebnis führt. Bei der Ermittlung einer Wahrscheinlichkeit zeichnen wir ein Baumdiagramm und wenden die Pfadregel an.
Wenn wir die Wahrscheinlichkeit eines Ereignisses suchen, genügt es, nur die Pfade zu zeichnen, die zu diesem Ereignis gehören. Dann wenden wir die Pfadregel an und addieren die Wahrscheinlichkeiten dieser Pfade.
Es gibt zwei Arten von Pfadregeln: die Produktregel und die Summenregel. Die Produktregel besagt, dass die Wahrscheinlichkeit eines einzelnen Ergebnisses das Produkt der Wahrscheinlichkeiten entlang des Pfades ist. Die Summenregel besagt, dass die Wahrscheinlichkeit eines Ereignisses die Summe der Wahrscheinlichkeiten der Pfade ist, die zu diesem Ereignis gehören.
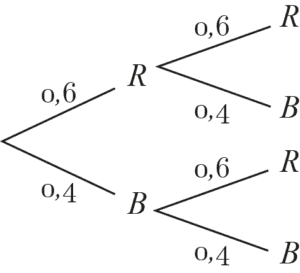
Um die Pfadregel zu verdeutlichen, betrachten wir das oben genannte Beispiel:
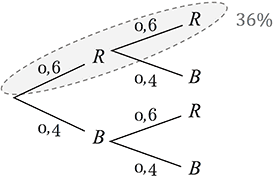
Die gesuchte Wahrscheinlichkeit, zwei rote Kugeln hintereinander zu ziehen, beträgt:
Die Wahrscheinlichkeit, eine rote und eine blaue Kugel zu ziehen, wird mit der Summenregel bestimmt:
Das Baumdiagramm und die Pfadregel sind mächtige Werkzeuge, um komplexe Wahrscheinlichkeiten zu berechnen. Nutze sie, um deine Chancen in verschiedenen Szenarien zu analysieren!