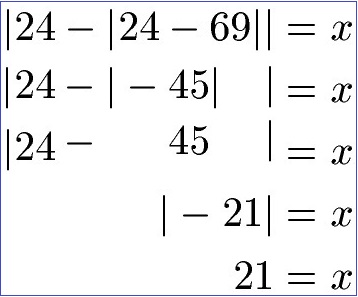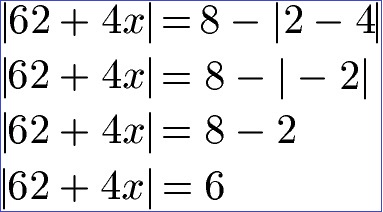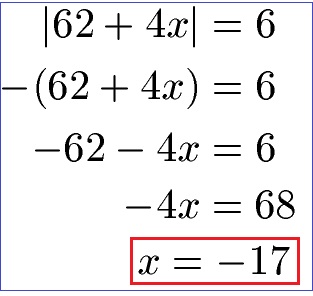Herzlich willkommen! Heute befassen wir uns mit Betragsgleichungen und wie man sie löst. Lasst uns direkt einsteigen:
Was sind Betragsgleichungen?
Eine Betragsgleichung beinhaltet einen oder mehrere Beträge. Bevor wir uns mit der Lösung solcher Aufgaben beschäftigen, werfen wir einen Blick darauf, was “Betrag” eigentlich bedeutet. Ein einfaches Beispiel verdeutlicht das Konzept: Der Betrag von +5 und -5 ist immer +5.
Betragsgleichung mit einem Betrag
Nehmen wir uns zunächst eine Betragsgleichung mit einem Betrag vor. Wie lautet die Lösung dieser Aufgabe?
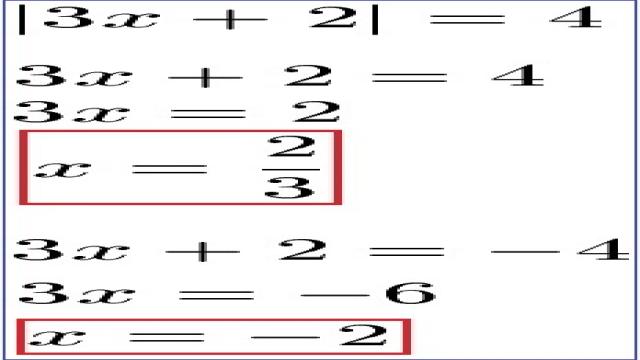
- Möglichkeit 1: 3x + 2 = 4
- Möglichkeit 2: 3x + 2 = -4
Der Betrag von 4 ist 4, aber auch der Betrag von -4 ist 4.
Wie lösen wir das? Eine Möglichkeit besteht darin, die Ausgangsformulierung in zwei Gleichungen aufzuteilen. Das bedeutet, dass entweder 3x + 2 = 4 oder 3x + 2 = -4 gilt. Diese beiden Gleichungen können wir einfach lösen.
Das Ergebnis kann entweder -2 oder +0,66666… sein.
Betragsgleichung mit mehreren Beträgen
Jetzt schauen wir uns Betragsgleichungen mit mehreren Beträgen an. Dabei behandeln wir sowohl “einfache” Betragsgleichungen ohne Variablen als auch solche mit Variablen.
- Beispiel 2: Gleichung mit 2 Beträgen
- Beispiel 3: Betragsgleichung mit mehreren Beträgen
Bei Beispiel 2 berechnen wir zunächst 24 – 69 = -45 und nehmen davon den Betrag von +45, wobei das Minuszeichen vor dem Betragsstrich erhalten bleibt. Anschließend rechnen wir 24 – 45 = -21 und nehmen davon den Betrag von +21. Somit ergibt sich x = 21 als Lösung.
In Beispiel 3 haben wir links und rechts vom Gleichheitszeichen einen Betrag. Wie groß ist x?
Zunächst vereinfachen wir die rechte Seite der Gleichung.
Anschließend führen wir eine Fallunterscheidung durch. Dazu lassen wir beim Betrag die Betragszeichen weg und lösen die Gleichung wie gewohnt auf. Wir bringen die 4x auf die rechte Seite und alle Zahlen auf die linke Seite.
Wir erhalten x = -14 als erste Lösung. Doch es gibt noch einen zweiten Fall: Wir setzen das, was zwischen den Betragsstrichen steht, in Klammern und davor ein Minuszeichen. Damit ändern sich alle Vorzeichen in der Klammer. Anschließend lösen wir erneut nach x auf.
Für den zweiten Fall erhalten wir x = -17 als Lösung. Das bedeutet, dass die Betragsgleichung sowohl mit x = -14 als auch mit x = -17 korrekt gelöst wird.
Aufgaben / Übungen
Du hast noch keine der fünf Aufgaben erfolgreich gelöst.
Video Betragsgleichungen
Hier ist ein Video, das dir Betragsgleichungen anschaulich erklärt:
[