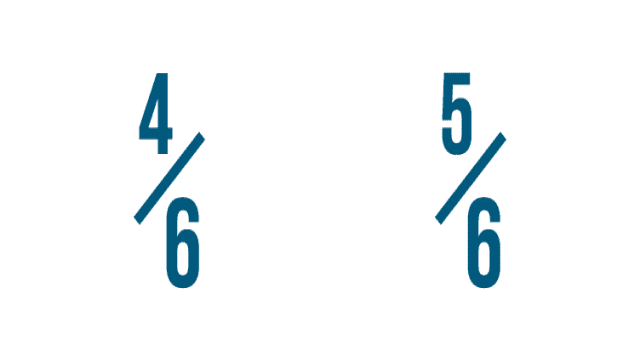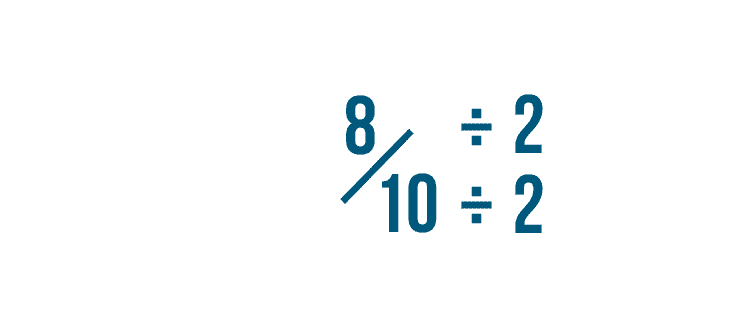Willkommen zu unserem Artikel über Bruchrechnen! Brüche sind eine großartige Möglichkeit, um Teile von etwas darzustellen und genau anzugeben, wie viel wir davon haben. Manche Brüche sind größer als andere. Zum Beispiel, welcher Bruch ist größer: 6/8 oder 7/8?
In diesem Bild können wir sehen, dass 7/8 größer ist. Die Abbildung erleichtert den Vergleich dieser Brüche. Aber wie könnten wir es ohne die Bilder gemacht haben?
Vergleich von Brüchen
In der Einführung zu Brüchen haben wir gelernt, dass Brüche aus zwei Teilen bestehen. Ein Teil ist die obere Zahl, auch Zähler genannt. Der andere Teil ist die untere Zahl, auch Nenner genannt. Der Nenner gibt uns an, wie viele Teile ein Ganzes hat, während der Zähler uns zeigt, wie viele dieser Teile wir haben.
Wenn Brüche den gleichen Nenner haben, bedeutet dies, dass sie in die gleiche Anzahl von Teilen aufgeteilt sind. Das bedeutet, dass wir diese Brüche einfach durch Betrachten des Zählers vergleichen können. Wenn der Zähler größer ist, ist der Bruch größer.
Hier ist 5 größer als 4, also können wir sagen, dass 5/6 größer ist als 4/6.
Schauen wir uns ein weiteres Beispiel an. Welcher dieser Brüche ist größer: 2/8 oder 6/8?
Wenn du gedacht hast, dass 6/8 größer ist, hast du recht! Beide Brüche haben den gleichen Nenner. Daher vergleichen wir einfach die Zähler. Da 6 größer ist als 2, ist 6/8 größer als 2/8.
Das war einfach, oder? Wenn zwei oder mehr Brüche den gleichen Nenner haben, kannst du sie vergleichen, indem du dir nur die Zähler ansiehst. Je größer der Zähler, desto größer ist der Bruch.
Vergleich von Brüchen mit unterschiedlichen Nennern
Auf der vorherigen Seite haben wir Brüche verglichen, die den gleichen Nenner haben. Aber du weißt, dass Brüche jeden beliebigen Nenner haben können. Was passiert, wenn du Brüche mit unterschiedlichen Nenner vergleichen musst?
Lass uns diese Brüche vergleichen: 5/8 und 4/6. Bevor wir sie vergleichen können, müssen wir beide Brüche so ändern, dass sie den gleichen Nenner haben.
Unser erster Schritt besteht darin, die kleinste Zahl zu finden, die beiden Nennern geteilt werden kann. Wir nennen das den niedrigsten gemeinsamen Nenner. In diesem Fall ist das 24.
Um 5/8 in 24stel umzuwandeln, multiplizieren wir den Nenner mit 3. Das bedeutet, dass wir auch den Zähler um 3 multiplizieren müssen. 5 mal 3 ergibt 15. Also haben wir 5/8 in 15/24 geändert.
Um 4/6 in 24stel umzuwandeln, multiplizieren wir den Nenner mit 4. Das bedeutet, dass wir auch den Zähler um 4 multiplizieren müssen. 4 mal 4 ergibt 16. Also haben wir 4/6 in 16/24 geändert.
Jetzt, da die Nenner gleich sind, können wir die Brüche vergleichen, indem wir uns die Zähler ansehen. 16/24 ist größer als 15/24, also ist 4/6 größer als 5/8.
Wie du siehst, haben wir die Brüche verglichen, indem wir sie auf den gleichen Nenner gebracht haben. Das macht es viel einfacher, sie zu vergleichen.
Reduzieren von Brüchen
Welcher von diesen Brüchen ist größer: 4/8 oder 1/2?
Wenn du die Mathematik gemacht oder sogar nur das Bild angesehen hast, hast du vielleicht erkannt, dass sie gleich sind. Mit anderen Worten, 4/8 und 1/2 bedeuten dasselbe, obwohl sie unterschiedlich geschrieben sind.
Wenn 4/8 dasselbe bedeutet wie 1/2, warum nennen wir es nicht einfach so? “Einhalb” ist einfacher zu sagen als “vier-achtel” und für die meisten Menschen auch leichter zu verstehen. Schließlich teilst du die Rechnung mit einem Freund in der Hälfte, nicht in Achtel.
Wenn du 4/8 als 1/2 schreibst, reduzierst du es. Wenn wir einen Bruch reduzieren, schreiben wir ihn in einer einfacheren Form auf. Reduzierte Brüche sind immer gleich dem ursprünglichen Bruch.
Wir haben 4/8 bereits auf 1/2 reduziert. Wenn du dir die Beispiele unten ansiehst, kannst du sehen, dass auch andere Zahlen auf 1/2 reduziert werden können. Diese Brüche sind alle gleich.
5/10 = 1/2
11/22 = 1/2
36/72 = 1/2
Diese Brüche wurden ebenfalls auf eine einfachere Form reduziert.
4/12 = 1/3
14/21 = 2/3
35/50 = 7/10
Wie du gesehen hast, wenn zwei oder mehr Brüche den gleichen Nenner haben, kannst du sie vergleichen, indem du dir ihre Zähler ansiehst. Je größer der Zähler, desto größer der Bruch.
Bruchrechnen kann zunächst einschüchternd wirken, aber es ist gar nicht so schwer. Indem wir Brüche vergleichen, reduzieren und in gemischte Zahlen umwandeln, können wir Brüche besser verstehen und mit ihnen arbeiten. Viel Spaß beim Üben und viel Erfolg beim Bruchrechnen!