Die lineare Regression ist eines der vielseitigsten statistischen Verfahren und bietet verschiedene Anwendungsmöglichkeiten. In diesem Artikel werden wir uns eingehend mit dem Thema der linearen Regression beschäftigen und uns insbesondere auf die einfache lineare Regression konzentrieren. Dabei geht es darum, wie Beziehungen zwischen zwei Variablen beschrieben und modelliert werden können. Keine Sorge, wir werden komplexe Formeln vermeiden und die Erklärung einfach und verständlich gestalten!
Lineare Regression einfach erklärt mit Praxisbeispiel
Stellen Sie sich vor, die Firma Kuschelwuschel hat ein neues Haarwuchsmittel entwickelt und möchte nun eine Studie durchführen, um das Haarwachstum unter Verwendung dieses Mittels quantitativ zu erfassen und vorherzusagen.
Zunächst werden die Zusammenhänge zwischen den Variablen grafisch mit Streudiagrammen dargestellt. Anschließend werden Schätzwerte für die Effekte und Tests auf signifikante Effekte berechnet. In unserem Beispiel verwenden wir das Programm SPSS von IBM zur Durchführung und Interpretation der linearen Regression.
Diese Fragen werden in diesem Artikel beantwortet:
- Wofür benötigt man eine lineare Regression?
- Was sind kleinste Quadrate (KQ)?
- Was versteht man unter einem Streudiagramm?
- Wie gut beschreibt die Regressionsgerade die Daten?
- Wie erkennt man, ob eine Einflussvariable signifikant ist?
- Was muss man bei der linearen Regression beachten?
- Was versteht man unter dem Begriff “multiple lineare Regression”?
Eine haarige Angelegenheit und eine lineare Regression
Unsere Kopfhaare wachsen im Jahr durchschnittlich um 13 cm. Doch diese Aussage allein reicht nicht aus, um den Zusammenhang zwischen verschiedenen Einflussfaktoren und dem Haarwachstum zu verstehen. Es gibt viele Faktoren, die das Haarwachstum beeinflussen, wie z.B. Jahreszeit, Geschlecht, Haarpflege, Alter, genetische Disposition und viele mehr.
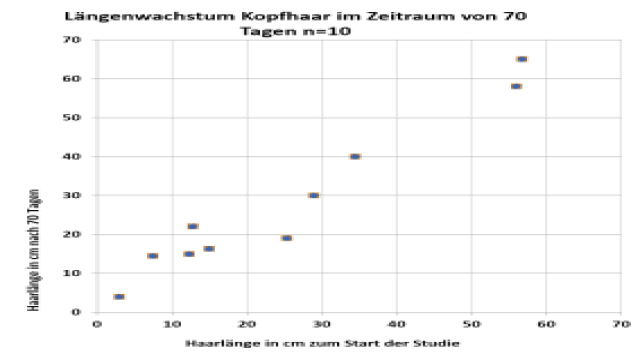
In einer Studie von Kuschelwuschel wurden die Haarlängen von 10 Probanden, die mit einem innovativen Shampoo behandelt wurden, gemessen. Die Messwerte wurden in einem Streudiagramm veranschaulicht. Es zeigt sich ein positiver linearer Zusammenhang zwischen der Ausgangslänge der Haare und dem Wachstum in einem bestimmten Zeitraum. Der Pearson-Korrelationskoeffizient beträgt r = 0,973.
Nach welchen Kriterien legt man eine optimale Gerade durch die Punktewolke?
Eine Gerade durch die Punktewolke wird durch die Formel Y = a + b * X beschrieben. Dabei steht a für den y-Achsenabschnitt und b für die Steigung der Regressionsgeraden. Die optimale Gerade wird so durch den Punkt (durchschnittliche Ausgangslänge der Haare, durchschnittliches Wachstum) gelegt, dass die Abweichung der beobachteten Werte von den vorhergesagten Werten minimal ist. Dieses Verfahren wird als Methode der kleinsten Quadrate bezeichnet. Die Gerade mit der geringsten Summe der quadrierten Abweichungen ist die optimale Regressionsgerade.
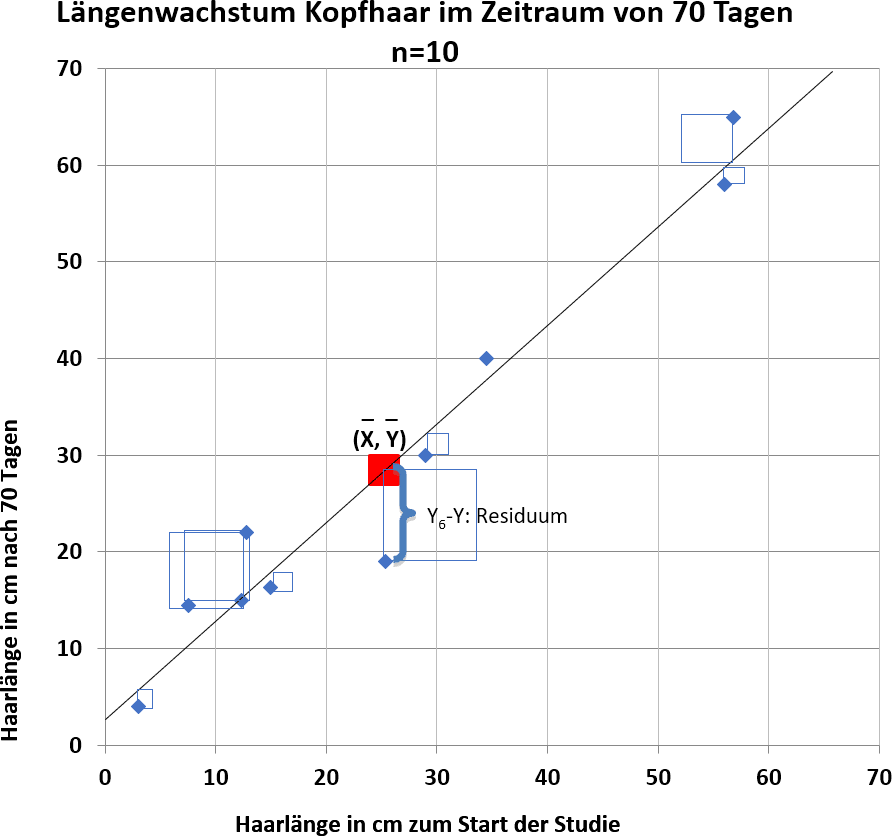
Residuen Quadrate bei optimaler Regressionsgerade
Lineare Regression einfach erklärt mit SPSS
Um die lineare Regression mit SPSS durchzuführen, werden die Messwerte in das Programm eingegeben. Anschließend wählt man den Menüpunkt “Analysieren – Regression – Linear”. Die abhängige Variable sind die Haarlängen nach der Behandlung, während die unabhängige Variable die Ausgangslänge der Haare ist. SPSS berechnet dann Schätzwerte für den y-Achsenabschnitt und die Steigung der Regressionsgeraden.
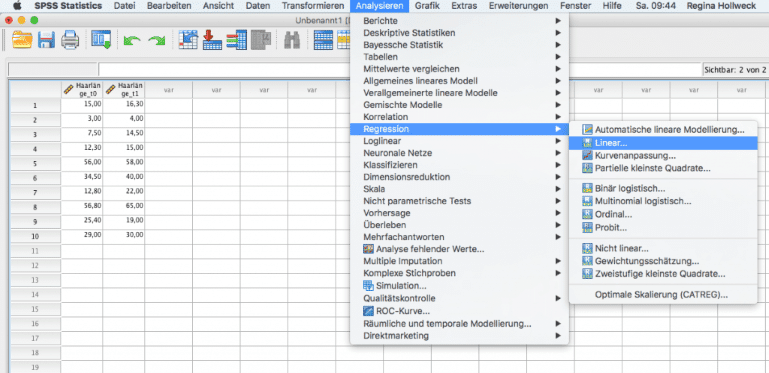
Aufruf der linearen Regression in SPSS
So interpretiert man eine lineare Regression mit SPSS
Die Ausgabe von SPSS enthält verschiedene Tabellen. In der Tabelle “Modellzusammenfassung” werden Maßzahlen für die Modellgüte angegeben. Das Bestimmtheitsmaß R2 gibt an, wie gut das Modell die Daten beschreibt. Ein Wert von 1 bedeutet, dass alle Punkte genau auf der Regressionsgeraden liegen. Je näher der Wert bei 1 liegt, desto besser passt das Modell zu den Daten.
In der Tabelle “ANOVA” wird getestet, ob das Modell signifikant ist. Bei einem p-Wert von weniger als 0,05 kann man davon ausgehen, dass es einen signifikanten Effekt der unabhängigen Variable auf die abhängige Variable gibt. In der Tabelle “Koeffizienten” werden die Schätzwerte für den y-Achsenabschnitt und die Steigung der Regressionsgeraden angegeben.
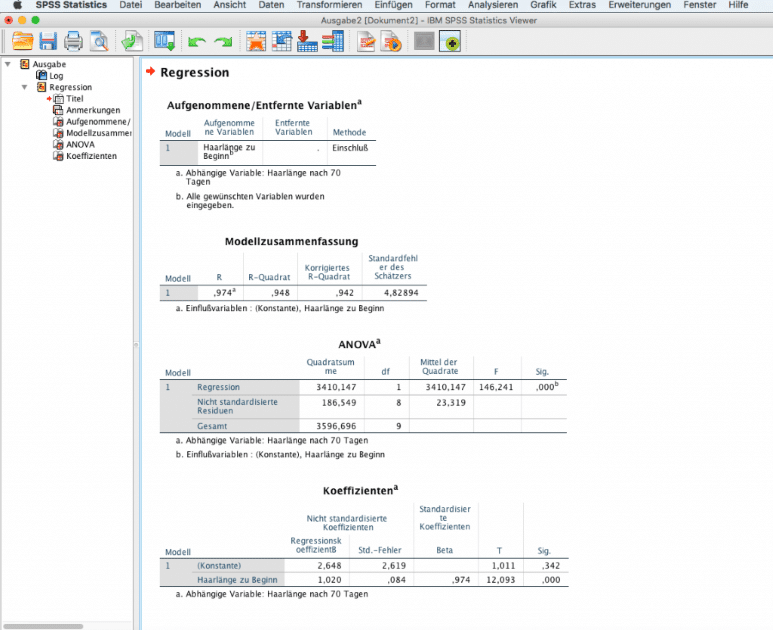
Ausgabefenster SPSS der linearen Regression
Voraussetzungen für lineare Regression einfach erklärt
Es gibt drei Hauptvoraussetzungen für die Durchführung einer linearen Regression:
- Die Residuen müssen voneinander unabhängig sein.
- Die Residuen sollten ungefähr einer Normalverteilung folgen.
- Die Streuung der Residuen sollte über den gesamten Wertebereich der abhängigen Variable konstant sein.
Diese Voraussetzungen können mit verschiedenen statistischen Tests und grafischen Methoden überprüft werden.
Zusammenfassung: Lineare Regression einfach erklärt
Die lineare Regression ist ein nützliches statistisches Verfahren zur Beschreibung von Beziehungen zwischen Variablen. Sie ermöglicht die Vorhersage von Werten basierend auf bekannten Daten. Die Durchführung der linearen Regression erfordert die Überprüfung von Voraussetzungen wie Linearität, Unabhängigkeit der Residuen, Normalverteilung und konstanter Streuung der Residuen. Mit Hilfe von SPSS können Schätzwerte für die Regressionskoeffizienten berechnet und signifikante Effekte getestet werden.
Für weitere Informationen zur linearen Regression oder anderen statistischen Themen stehen unsere Experten von Novustat gerne zur Verfügung.
Translation:
Linear regression is one of the most versatile statistical procedures. It is useful for making predictions, such as forecasting visitor numbers, as well as for investigating relationships, such as the impact of advertising expenses on sales volume. In this article, we will take a closer look at linear regression, focusing primarily on simple linear regression: how can the relationship between two variables be described and modeled? We will explain these concepts in a simple and understandable way, avoiding complicated formulas!
Simple Linear Regression with a Practical Example
Let’s imagine the following situation: The company Kuschelwuschel has developed a new hair growth product after years of research. Now, they want to conduct a study to clinically examine the effects of this product on hair growth. To quantify and predict hair growth based on the data collected, we will first create scatter plots to visualize the relationships. Then, using SPSS software by IBM, we will perform and interpret the linear regression analysis.
This Article Answers the Following Questions:
- Why is linear regression necessary?
- What are the least squares?
- What is a scatter plot?
- How well does the regression line describe the data?
- How can we determine if an independent variable is significant?
- What are the requirements for linear regression analysis?
- What is multiple linear regression?
Hair Growth and Linear Regression
On average, our head hair grows 13 cm per year. However, this deterministic statement with precise correlations does not fully reflect reality. Various factors, such as season, gender, hair care, weather conditions, age, and genetic disposition, influence the growth rate. Furthermore, unpredictable measurement errors or interfering variables can introduce a significant amount of randomness.
To understand and describe the relationships between variables, let’s consider the hair length measurements of 10 participants in the Kuschelwuschel study. The participants were treated with the innovative shampoo developed by the company:

Hair Lengths of 10 Participants
These measurements can be visualized in a scatter plot, with the independent variable (X) representing the initial hair length and the dependent variable (Y) representing the hair length after 70 days of treatment.
How to Determine the Best-Fitting Line?
A regression line can be defined by the equation Y = a + b * X, where a represents the y-intercept and b represents the slope of the regression line. To find the best-fitting line, we minimize the sum of squared residuals – the differences between the observed Y values and the predicted Y values on the regression line. This method is called the method of least squares. The optimal regression line is the one with the smallest sum of squared residuals.

Residual Squares with Optimal Regression Line
Simple Linear Regression with SPSS
To perform linear regression analysis with SPSS, we enter the 10 hair length measurements into the software. Then, we select “Analyze – Regression – Linear” from the menu. The dependent variable is the hair length at the end of the study, and the independent variable is the initial hair length. SPSS will calculate the estimates for the y-intercept and slope of the regression line.

Calling Linear Regression in SPSS
Interpreting Linear Regression with SPSS
The SPSS output includes several tables. The “Model Summary” table provides measures of the model fit. R represents the Pearson correlation coefficient, while R-squared indicates the proportion of variance in the data explained by the model. R-squared ranges from 0 to 1, with a value of 1 indicating a perfect fit. Adjusted R-squared is a modification that takes into account the number of predictor variables. In this example, with only one predictor variable, adjusted R-squared is not relevant.
The “ANOVA” table performs an F-test to determine if the model is significant. If the p-value is less than 0.05, we can conclude that there is a significant effect of the independent variable on the dependent variable. The “Coefficients” table provides estimates for the y-intercept and slope of the regression line.

SPSS Output of Linear Regression
Assumptions for Linear Regression
There are three main assumptions for linear regression analysis:
- Independence of residuals: The residuals should be independent of each other.
- Normality of residuals: The residuals should follow a roughly normal distribution.
- Homoscedasticity: The variance of the residuals should be constant across all levels of the dependent variable.
These assumptions can be assessed using statistical tests and graphical methods.
Summary: Linear Regression Explained Simply
Linear regression is a useful statistical technique for describing relationships between variables. It allows us to predict values based on known data. To perform linear regression analysis, we need to check assumptions such as linearity, independence of residuals, normality, and constant variance of residuals. SPSS can calculate estimates for the regression coefficients and test for significant effects.
For further information on linear regression or any other statistical topics, feel free to contact our experts at Novustat.
End Translation