Die Statistik ist eine faszinierende Wissenschaft, die uns hilft, Informationen aus Daten zu gewinnen. Ein wichtiger Teil davon sind statistische Tests, die es uns ermöglichen, Hypothesen auf ihre Gültigkeit zu überprüfen. In diesem Artikel werden wir uns mit zwei wichtigen Konzepten befassen: dem kritischen Wert und dem p-Wert.
Was ist der kritische Wert?
Der kritische Wert ist ein Schwellenwert, der den Annahmebereich eines statistischen Tests vom Ablehnungsbereich trennt. Wenn wir eine Hypothese überprüfen, nehmen wir an, dass unsere Stichprobenergebnisse zufälligen Schwankungen unterliegen. Wir formulieren eine Nullhypothese, die besagt, dass es keinen Unterschied oder Zusammenhang gibt. Unter dieser Annahme können wir bestimmen, wie wahrscheinlich unsere Stichprobenergebnisse im Vergleich zu einem bestimmten Wert eintreten.
Nehmen wir an, wir haben eine Stichprobe von Körpergrößen von Frauen. Wir möchten überprüfen, ob der Durchschnitt kleiner ist als ein bestimmter Wert. Der kritische Wert gibt uns den Grenzwert an, unterhalb dessen die Stichprobenergebnisse liegen müssen, um die Nullhypothese zu akzeptieren. Wenn unsere Teststatistik diesen kritischen Wert überschreitet, verwerfen wir die Nullhypothese. Andernfalls können wir die Nullhypothese nicht ablehnen.
Annahmebereich und Ablehnungsbereich
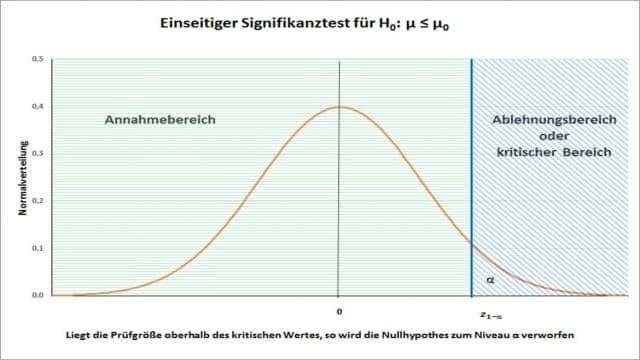
Der Annahmebereich enthält alle Werte, die wir akzeptieren, wenn die Nullhypothese gilt, während der Ablehnungsbereich alle Werte enthält, bei denen wir die Nullhypothese verwerfen. Der Annahmebereich wird in der Grafik grün schraffiert dargestellt, während der Ablehnungsbereich blau schraffiert ist.
In unserem Beispiel der Körpergröße von Frauen ist der Annahmebereich der Bereich, in dem der Durchschnitt größer oder gleich dem kritischen Wert ist. Der Ablehnungsbereich umfasst alle Durchschnittswerte, die kleiner als der kritische Wert sind. Je nachdem, in welchem Bereich unsere Teststatistik liegt, können wir die Nullhypothese akzeptieren oder verwerfen.
Zweiseitiges Testen und der p-Wert
In einigen Fällen möchten wir nicht nur überprüfen, ob der Durchschnitt größer oder kleiner ist, sondern ob es einen signifikanten Unterschied in beide Richtungen gibt. In solchen Fällen verwenden wir einen zweiseitigen Test.
Ein zweiseitiger Test hat sowohl einen Annahmebereich als auch einen Ablehnungsbereich auf beiden Seiten der Verteilung. Der kritische Wert wird so gewählt, dass die Wahrscheinlichkeit, dass die Teststatistik in den Ablehnungsbereich fällt, bei einer vorgegebenen Signifikanzschwelle (meist α = 0,05) liegt.
Ein alternativer Ansatz zur Testentscheidung ist die Verwendung des p-Werts. Der p-Wert gibt die Wahrscheinlichkeit an, dass unsere Teststatistik oder ein extremere Wert unter der Nullhypothese auftritt. Wenn der p-Wert kleiner als die vorgegebene Signifikanzschwelle ist, verwerfen wir die Nullhypothese. Andernfalls können wir die Nullhypothese nicht ablehnen.
Zusammenfassung
Der kritische Wert und der p-Wert sind wichtige Konzepte in der statistischen Hypothesentestung. Sie helfen uns, unsere Nullhypothese zu überprüfen und statistisch signifikante Ergebnisse zu erlangen. Der kritische Wert trennt den Annahmebereich vom Ablehnungsbereich, während der p-Wert uns sagt, wie wahrscheinlich unsere Teststatistik unter der Nullhypothese ist.
Statistik kann komplex sein, aber mit diesen Konzepten und Werkzeugen können wir Daten besser verstehen und fundierte Entscheidungen treffen. Also, lass uns weiter tüfteln und die Geheimnisse der Statistik entschlüsseln!
Bitte beachte, dass dieser Artikel nur eine Einführung in die Thematik darstellt und weitere Studien erforderlich sind, um ein tieferes Verständnis zu erlangen.
Quellen: