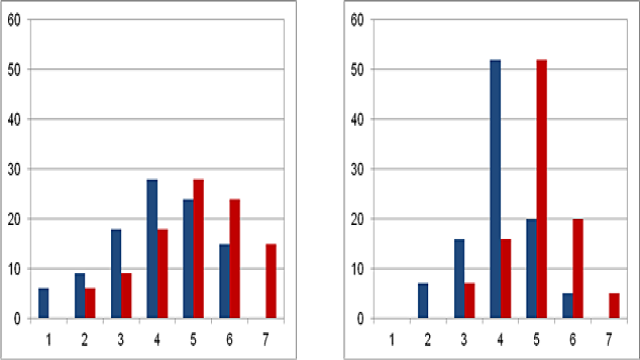
Statistische Tests sind ein wichtiger Bestandteil der Datenanalyse, insbesondere wenn es darum geht, Unterschiede zwischen Gruppen zu untersuchen. Ein beliebter Test für den Vergleich von Mittelwerten ist der t-Test für unverbundene Stichproben. Erfahren Sie in diesem Artikel, wie Sie diesen Test richtig anwenden und interpretieren können.
Warum der t-Test so wichtig ist
Der t-Test ist einer der bekanntesten statistischen Tests und wird häufig verwendet, um festzustellen, ob die Mittelwerte von metrischen Merkmalen in zwei Gruppen signifikant voneinander abweichen. Stellen Sie sich vor, Sie möchten die Kaufabsicht für ein neues Produkt untersuchen und vergleichen, ob es Unterschiede zwischen männlichen und weiblichen Befragten gibt. Der t-Test kann Ihnen dabei helfen, diese Frage zu beantworten.
Wie funktioniert der t-Test?
Der t-Test basiert auf der Annahme, dass die Mittelwerte in den beiden Gruppen gleich sind. Der p-Wert, der das Ergebnis des t-Tests ist, gibt an, mit welcher Wahrscheinlichkeit die Hypothese gleicher Mittelwerte verworfen werden kann. Ist der p-Wert kleiner als ein vorgegebenes Signifikanzniveau (in der Regel 0,05), wird der Unterschied als signifikant angesehen.
Die Konstruktion der Teststatistik
Um den t-Test durchzuführen, wird eine Teststatistik berechnet, die auf der Differenz der Mittelwerte basiert. Diese Teststatistik folgt einer t-Verteilung und hilft dabei, den p-Wert zu bestimmen. Die Berechnung der Teststatistik berücksichtigt auch die Standardabweichung und die Größe der Stichprobe. Je größer die Differenz der Mittelwerte ist, je kleiner die Standardabweichung und je größer die Stichprobe, desto wahrscheinlicher ist ein signifikanter Unterschied.
Voraussetzungen für den t-Test
Damit der t-Test gültige Ergebnisse liefert, gibt es einige Voraussetzungen zu beachten. Die Größe der Stichprobe sollte in beiden Gruppen mindestens 30 betragen, um von einer Normalverteilung auszugehen. Wenn die Stichprobenumfänge unterschiedlich sind oder sich die Varianzen in den Gruppen deutlich unterscheiden, sollte der Welch-Test verwendet werden, eine Variante des t-Tests.
Zusammenfassung
Der t-Test ist ein wertvolles Werkzeug, um Mittelwertunterschiede zwischen Gruppen zu untersuchen. Mit diesem Test können Sie herausfinden, ob die Unterschiede signifikant sind und somit statistisch relevant. Vergessen Sie jedoch nicht, die Voraussetzungen für den t-Test zu überprüfen, um valide Ergebnisse zu erhalten.
Bildnachweise:
Literatur:
- Bortz, J.; Schuster, C.: Tests zur Überprüfung von Unterschiedshypothesen. In: Statistik für Human- und Sozialwissenschaftler, 7. Auflage, Berlin, 2010, S. 117-136.
- Lüken, J.; Schimmelpfennig, H.: Einführung in Signifikanztests. In: planung & analyse, Jg. 39/2012, Nr. 5, S. 24.
Mit diesen Informationen sind Sie nun bestens gerüstet, um den t-Test für Mittelwertvergleiche erfolgreich anzuwenden. Viel Erfolg bei Ihrer Datenanalyse!