Für viele statistische Auswertungen spielt die Wahrscheinlichkeitsverteilung eine entscheidende Rolle. Egal, ob Sie Daten für eine Qualitätskontrolle, eine Analyse der Kundenzufriedenheit oder die Optimierung von Produktionskapazitäten auswerten, das Verständnis der jeweiligen Wahrscheinlichkeitsverteilung ist unerlässlich! In diesem Artikel zeigen wir Ihnen die fünf wichtigsten Verteilungen und geben Ihnen praktische Beispiele. Bei Fragen zur Wahrscheinlichkeitsverteilung und Datenanalyse steht Ihnen unsere Statistik Hilfe gerne zur Verfügung!
1 – Normalverteilung: die wichtigste Wahrscheinlichkeitsverteilung
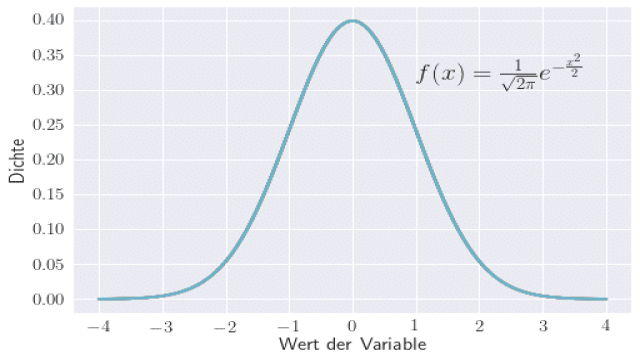
Die Normalverteilung oder Gauß-Verteilung ist die wichtigste Wahrscheinlichkeitsverteilung. Sie stellt eine stetige Verteilung dar und kann alle reellen Zahlen annehmen. Die Dichtefunktion wird durch die Gaußsche Glockenkurve beschrieben, wobei der Mittelwert (µ) und die Standardabweichung () Parameter der Normalverteilung sind.
Anwendung
Die Normalverteilung findet in verschiedenen Bereichen Anwendung. Beispiele sind biologische Größen wie Körpergrößen, Intelligenzquotienten oder Sozialkompetenz, physikalische Sachverhalte wie die Sonnenscheindauer an bestimmten Tagen des Jahres, statistische Fehler bei Regressionsanalysen oder im Zusammenhang mit statistischen Tests sowie Qualitätskontrollen wie die Dicke eines Brettes in einer Sägerei. Ein weiterer wichtiger Aspekt ist der zentrale Grenzwertsatz, der besagt, dass unter bestimmten Voraussetzungen die Summe unabhängiger, identisch verteilter Zufallsvariablen wiederum normalverteilt ist.
2 – t-Verteilung: Normalverteilung für kleine Stichprobengrößen
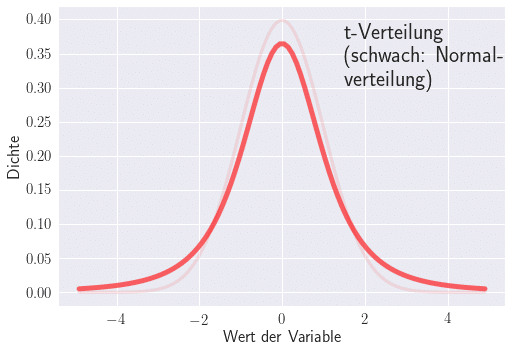
Die t-Verteilung wird verwendet, wenn die Normalverteilung bei kleinen Stichprobenumfängen bestimmte statistische Größen unterschätzt. Die t-Verteilung ähnelt der Normalverteilung, hat jedoch breitere Enden. Für größere Stichprobenumfänge nähern sich die beiden Verteilungen an und sind schließlich identisch.
Anwendung
Die t-Verteilung spielt eine wichtige Rolle bei statistischen Analysen, insbesondere bei Hypothesentests und Konfidenzintervallen. Wenn die Varianz unbekannt ist und durch die Stichprobenvarianz geschätzt wird, ist der Mittelwert der Stichprobe t-verteilt mit n−1 Freiheitsgraden.
3 – Poisson-Verteilung: Modellierung von Zählgrößen
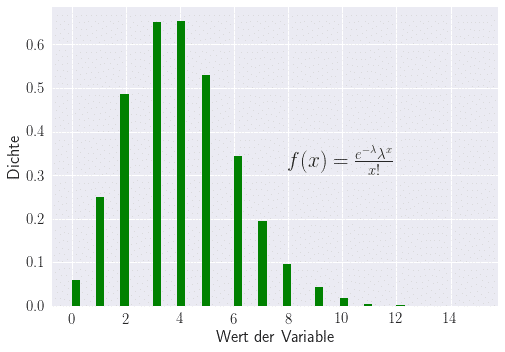
Die Poisson-Verteilung beschreibt diskrete Wahrscheinlichkeitsverteilungen und modelliert die Verteilung von Zählgrößen. Sie gibt an, wie oft ein bestimmtes zählbares Ereignis eintritt, wenn es häufig wiederholt wird. Der Parameter μ steht für die mittlere Ereignisrate.
Anwendung
Die Poisson-Verteilung findet Anwendung in verschiedenen Bereichen, z.B. bei der Anzahl der Soldaten, die pro Jahr in der preußischen Armee durch einen Pferdetritt versehentlich getötet wurden, der Anzahl der Mutationen auf einem DNA-Strang pro Zeiteinheit oder der Anzahl der Besucher einer Website pro Minute, Stunde oder Tag.
4 – Exponentialverteilung: Modellierung von Wartezeiten
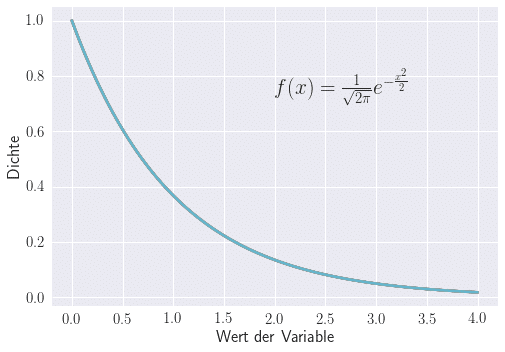
Die Exponentialverteilung beschreibt stetige Verteilungen, die zur Modellierung von zufälligen Zeitintervallen verwendet werden. Der Parameter λ steht für die Anzahl der erwarteten Ereignisse pro Zeitintervall.
Anwendung
Die Exponentialverteilung wird bei der Modellierung von Wartezeiten verwendet, z.B. bei der Lebensdauer von Menschen, Teilen von Maschinen oder der Zeit zwischen Anrufen in einem Callcenter. Sie wird auch zur Approximation der Lebensdauer von zerfallenden Teilchen in der Physik verwendet.
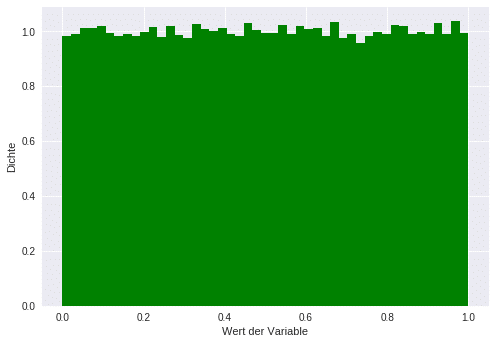
5 – Gleichverteilung: Modellierung von gleich wahrscheinlichen Ereignissen
Die Gleichverteilung ist eine besondere Art von Wahrscheinlichkeitsverteilung, bei der alle Werte gleich wahrscheinlich sind. Sie kann sowohl stetig als auch diskret sein.
Anwendung
Die Gleichverteilung wird bei Ereignissen verwendet, bei denen jeder Wert gleich wahrscheinlich ist. Ein Beispiel für eine diskrete Gleichverteilung ist ein fairer Würfel, bei dem jede Seite mit der gleichen Wahrscheinlichkeit auftritt. Ein Beispiel für eine stetige Gleichverteilung ist die Wartezeit auf einen alle 10 Minuten verkehrenden Bus, wenn man zu einer zufälligen Zeit an der Bushaltestelle ankommt.
Fazit – Das sollten Sie aus diesem Artikel mitnehmen
Wahrscheinlichkeitsverteilungen sind ein unersetzliches Werkzeug in der statistischen Analyse, um zufällige Ereignisse zu modellieren. In diesem Artikel wurden die fünf wichtigsten Verteilungen besprochen. Wenn Sie weitere Informationen zu anderen Verteilungen oder Unterstützung bei statistischen Arbeiten benötigen, stehen wir Ihnen gerne mit kompetenter Statistikberatung zur Seite!
Weiterführende Links:
[1] Liste von Wahrscheinlichkeitsverteilungen
[2] Dichtefunktion und Verteilungsfunktion
[3] Rechenbeispiel Normalverteilung