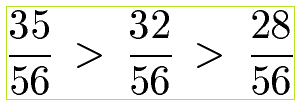Die Kunst des Bruchvergleichs

Habt ihr euch schon einmal gefragt, wie ihr Brüche vergleicht? In diesem Artikel werdet ihr lernen, wie es geht. Hier ist, was wir besprechen werden:

• Eine Erklärung, wie man Brüche vergleichbar macht.
• Viele Beispiele zum Vergleichen von Brüchen.
• Aufgaben und Übungen, damit ihr das Bruchvergleichen selbst üben könnt.
• Videos zur Bruchrechnung.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wenn ihr keine Ahnung von der Bruchrechnung habt, schaut euch bitte zuerst den Artikel “Bruchrechnen” an. Ansonsten zeigen wir euch nun, wie ihr Brüche vergleichen könnt.

Erklärung Brüche vergleichen

Manchmal fragt man sich in der Mathematik, ob ein Bruch kleiner oder größer ist als ein anderer Bruch. Bei zwei gleichnamigen Brüchen ist der Vergleich einfach. Gleichnamige Brüche haben den gleichen Nenner. In diesem Fall schaut man nur auf den Zähler. Der Bruch mit dem kleineren Zähler ist auch der kleinere Bruch.

• Beispiel 1: Welcher Bruch ist größer?
  Lösung: Wir haben zwei gleiche Nenner. Hier schauen wir nur auf den Zähler, um den größeren Bruch zu finden. Das Symbol “>” bedeutet größer.

• Beispiel 2: Was passiert, wenn die Zähler gleich sind?
  Lösung: Wenn die Zähler gleich sind und die Nenner unterschiedlich, ist der Bruch mit dem kleineren Nenner der größere Bruch.

Die letzte Regel zum Bruchvergleich werden wir im nächsten Abschnitt betrachten.

Beispiele Brüche vergleichen

Was passiert bei ungleichnamigen Brüchen? Wenn zwei oder mehr Brüche verschiedene Nenner haben? Hier ist ein einfacheres Beispiel:

• Beispiel 3: Vergleiche diese beiden Brüche und schreibe die kleinere Zahl nach links.
  Lösung: Die Brüche haben die Nenner 3 und 6. Um den Bruch mit dem Nenner 3 auf den Nenner 6 zu bringen, multiplizieren wir sowohl den Zähler als auch den Nenner mit 2. Der Zähler wird zu 4 und der Nenner zu 6. Nun sehen wir, dass 4 kleiner als 5 ist.

• Beispiel 4: Vergleiche drei Brüche mit unterschiedlichen Nennern. Der größte Bruch soll nach links geordnet werden, der kleinste Bruch nach rechts.
  Lösung: Die Brüche haben die Nenner 4, 7 und 8. Wir müssen einen gemeinsamen Hauptnenner finden, indem wir das kleinste gemeinsame Vielfache berechnen. Das kleinste gemeinsame Vielfache der Zahlen 4, 7 und 8 ist 56. Die Brüche werden mit 14, 8 und 7 erweitert. Nun vergleichen wir die Zähler, um die Größe der Brüche zu bestimmen.

Brüche vergleichen Übungsaufgaben

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Videos Brüche vergleichen

Fragen mit Antworten Brüche vergleichen