Die Verbindung zwischen Mathematik und Musik ist seit jeher faszinierend. Besonders interessant ist die Entdeckung der Pythagoräer, dass gleichgespannte Saiten harmonisch zusammenklingen, wenn ihre Längen in einem einfachen Verhältnis zueinander stehen. Heute drücken wir diese Harmonien lieber in Frequenzen aus und verwenden den Quintenzirkel, um sie zu visualisieren.
Quinten und andere Intervalle
In der Musik wird die Oktave als Frequenzverhältnis von 2 zu 1 definiert. Eine Quart entspricht 4 zu 3 und eine große Terz 5 zu 4. Mit diesen einfachen Brüchen können wir bereits einen Dur-Dreiklang erzeugen und die Grundlage für die westliche Musik schaffen. Das Verhältnis von 2 zu 1 klingt für unser Ohr besonders rein und angenehm.
Der Quintenzirkel
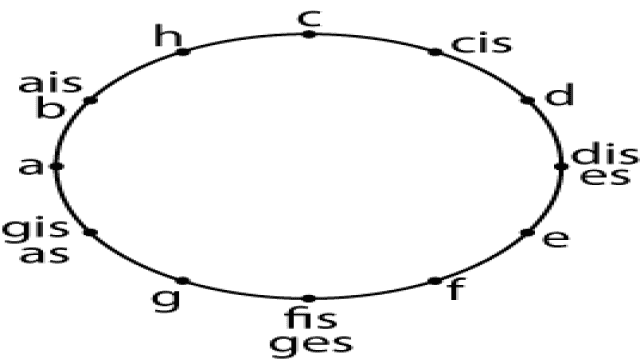
Wenn wir den Quintenzirkel betrachten, sehen wir, dass er auf dem C basiert und die zwölf Töne der chromatischen Tonleiter umfasst. Dieser Zirkel ist in der gleichschwebend temperierten Stimmung besonders relevant, da alle Töne gleichberechtigt sind. Traditionell haben einige Töne jedoch eine größere Bedeutung als andere. Die “weißen” Töne werden durch das Bilden von Quinten erzeugt, während die “schwarzen” Töne verschiedene Erzeugungswege haben und daher mit mehreren Namen leben müssen.
Die mathematische Struktur des Quintenzirkels
Mathematisch betrachtet ist der Quintenzirkel eine zyklische Gruppe, bei der ein einziges Element – die Zahl 1 oder das Zeitintervall einer Stunde – die gesamte Gruppe erzeugt. Wenn wir die Zahlen des Ziffernblatts einer Uhr verwenden, haben wir sowohl feste Zeitpunkte als auch Zeitintervalle. Dieses Konzept ermöglicht es uns, den Quintenzirkel als strukturiertes mathematisches Objekt zu betrachten.
Das Tonnetz und der Tönetorus
Um die komplexe Struktur des Quintenzirkels zu visualisieren, können wir das Tonnetz verwenden. Dabei ordnen wir den Quinten und Terzen Koordinaten zu und beschreiben jeden Ton entsprechend seiner Position im Netz. Alternativ können wir das Tonnetz auch auf einem Torus darstellen, einem dreidimensionalen Objekt, das die komplette Struktur des Zirkels enthält.
Die Anwendung des Quintenzirkels in der Musik
Der Quintenzirkel hat verschiedene Anwendungsbereiche in der Musik. Musiker können durch den Zirkel harmonische Übergänge und Tonartenwechsel besser verstehen und planen. Oft bewegen sich Harmonien in kleinen Schritten auf dem Tonnetz und wechseln zwischen Dur und Moll. Einige Übergänge sind besonders kurz und haben eine besondere klangliche Wirkung. Bei der Komposition von Stücken nutzen Musiker häufig diese Strukturen und Übergänge, um bestimmte Stimmungen zu erzeugen.
Fazit
Die Verbindung zwischen Mathematik und Musik ist faszinierend, aber nicht unbedingt der Hauptfokus der musikalischen Ausdrucksformen. Dennoch bietet die mathematische Struktur des Quintenzirkels eine interessante Perspektive und eine Möglichkeit, musikalische Harmonien zu analysieren und zu verstehen.
Das Original-Video “wie macht man das grose c auf der tonleiter” finden Sie hier.