Mathematische Konzepte wie Injektivität, Surjektivität und Bijektivität können oft für Verwirrung sorgen. Deshalb möchte ich sie hier anhand einer anschaulichen Prügelei erklären. Stellt euch vor, in einer Kneipe feiern einige Herren ausgelassen. Plötzlich taucht eine Gruppe wütender Amazonen auf und beginnt, die Männer zu verprügeln.
Was hat das alles mit Mathe zu tun, fragt ihr euch? Nun, die Amazonen repräsentieren die Menge X, während die Kerle die Menge Y darstellen. Jedes Mal, wenn eine Amazone einem Mann eine reinhaut, haben wir eine Funktion von X nach Y. Damit dies eine richtige Funktion ist, nehmen wir an, dass jede Amazone maximal einen Mann verprügelt.
Es gibt drei mögliche Szenarien:
Injektiv
Injektiv bedeutet anschaulich: Jeder y-Wert wird höchstens einem x-Wert zugeordnet! Bei unserer Prügelei bedeutet das, dass niemals zwei Amazonen denselben Mann verprügeln würden. Andernfalls gäbe es zwei x-Werte, die auf denselben y-Wert abbilden. Das wäre nicht injektiv! Es ist jedoch möglich, dass nicht alle Männer etwas abbekommen. Einige haben sich vielleicht hinter der Theke versteckt und entgehen so der Prügelei. Obwohl nicht alle Männer getroffen werden, ist die Funktion dennoch injektiv!
Surjektiv
Surjektiv ist die Prügelei, wenn wirklich jeder Mann etwas abbekommt. Das bedeutet, dass für jeden y-Wert mindestens ein x vorhanden ist, der auf diesen y-Wert abbildet. Wenn jedoch einer der Männer, sagen wir Helmut, sich hinter der Bar versteckt, ist unsere Prügelei nicht surjektiv. In diesem Fall gibt es einen y-Wert, der von keinem x erreicht wird. Beachtet, dass Surjektivität stark von der Menge Y abhängt. Wenn wir die Menge Y um einen Mann reduzieren, ändert sich nichts an der Prügelei, außer dass alle y-Werte getroffen werden. Surjektivität hängt also besonders von der Menge Y ab.
Bijektiv
Bijektiv ist die Prügelei, wenn jede Amazone genau einen Mann verprügelt und kein Mann verschont bleibt. Es gibt also eine Eins-zu-Eins-Beziehung: Jeder Mann wird von höchstens einer Amazone verprügelt und kein Mann bleibt übrig. Die Abbildung ist damit sowohl injektiv als auch surjektiv. Das bedeutet insbesondere, dass die Funktion umkehrbar ist! Die Männer, die ordentlich Prügel einstecken mussten, drehen den Spieß um und verprügeln die Amazonen in gleicher Weise. X bildet nun auf Y ab und natürlich wieder Eins-zu-Eins.
Nachdem die Männer den Frauen zurückgeschlagen haben, beschließen sie jedoch, dass Prügeln Unsinn ist, und entscheiden sich stattdessen, ein paar Biere zu trinken. Danach gehen sie gemeinsam nach Hause, um Liebe zu machen. Ob das noch bijektiv war oder ob möglicherweise mehrere x auf ein y kamen, kann ich euch leider nicht sagen. 😉
Nun wollen wir ein paar mathematische Beispiele durchgehen, um das Ganze zu veranschaulichen. Danach könnt ihr gerne in die Kneipe gehen.
Beispiel 1
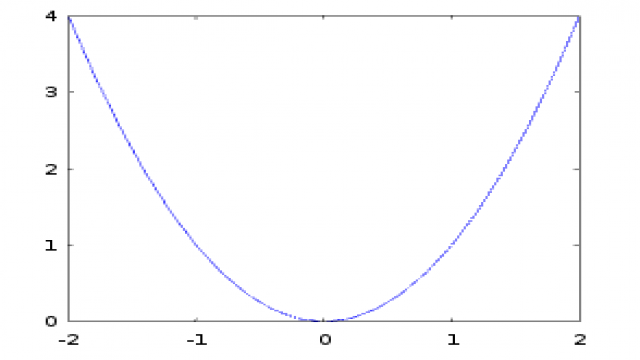
$$ f : mathbb{R} rightarrow mathbb{R},~~ f(x) = x^2 $$
Diese Funktion ist weder injektiv noch surjektiv! Denn alle y-Werte außer Null werden von zwei x-Werten erreicht (also nicht injektiv) und manche y-Werte werden gar nicht erreicht, nämlich alle negativen Zahlen (also nicht surjektiv). Wenn wir jedoch den Wertebereich auf $mathbb{R}{geq 0}$ ändern, ändert sich eigentlich nichts an der Funktion. Aber sie wird surjektiv (jedes y in $mathbb{R}{geq 0}$ wird erreicht). Damit die Funktion injektiv wäre, müssten wir den Definitionsbereich einschränken, zum Beispiel nur x-Werte zulassen, die größer oder gleich Null sind. Beachtet, dass dies eine echte Änderung an der Funktion ist.
Beispiel 2
$$ f : mathbb{R} rightarrow mathbb{R},~~ f(x) = e^x $$
Diese Funktion ist injektiv, aber nicht surjektiv. Wenn wir jedoch den Wertebereich auf $mathbb{R}{>0}$ ändern, ändert sich nichts an der Funktion. Sie wird dann bijektiv mit der Umkehrfunktion $f^{-1} : mathbb{R}{>0} rightarrow mathbb{R},~~ f^{-1}(x) = ln(x)$. Wiederum ist der Definitionsbereich von $f$ der Wertebereich von $f^{-1}$ und umgekehrt.
Beispiel 3
$$ f : mathbb{R} rightarrow mathbb{R},~~ f(x) = 5 $$
Diese Funktion ist weder surjektiv noch injektiv.
Beispiel 4
$$ f : mathbb{R} rightarrow mathbb{R},~~ f(x) = sin(x) $$
Auch diese Funktion ist weder surjektiv noch injektiv. Der Sinus kann jedoch surjektiv gemacht werden, indem wir den Bildbereich auf $[-1; 1]$ einschränken. Für Bijektivität müssten wir die Funktion wirklich verkleinern, zum Beispiel auf den Bereich $[-frac{pi}{2}; frac{pi}{2}]$.
Hinweise
Die Einschränkung des Definitionsbereichs, wie oben beschrieben, bedeutet eine Veränderung der Funktion. Deshalb wird dies oft explizit angegeben, zum Beispiel: $f|_{[-frac{pi}{2}; frac{pi}{2}]}$. So ist klar, dass es um die Einschränkung geht.