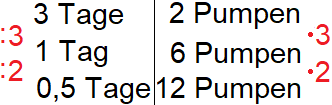Willkommen zu unserem Artikel über den Dreisatz! Hier erfährst du, was der Dreisatz ist und wie man damit rechnet. Wir werden uns ansehen:
- Eine Erklärung, welche Arten von Dreisatz es gibt und wie man damit rechnet.
- Beispiele, um den proportionalen und antiproportionalen Dreisatz anzuwenden.
- Aufgaben / Übungen, um dieses Thema selbst zu üben.
- Ein Video zum Dreisatz.
- Ein Frage- und Antwortbereich zu diesem Gebiet.
Hinweis: In diesem Artikel werden wir uns hauptsächlich auf die Grundlagen des Dreisatzes konzentrieren. Wenn du jedoch nur lernen möchtest, wie man Aufgaben der Prozentrechnung mit dem Dreisatz löst, dann schaue direkt in unseren Artikel “Prozentrechnung durch Dreisatz”.
Erklärung: Dreisatz proportional
Beginnen wir mit einer Definition für den Dreisatz:
Man unterscheidet in der Mathematik zwischen dem geraden und dem ungeraden Dreisatz. Die beiden Arten von Dreisatz lauten:
- Gerader Dreisatz: Wird auch als proportionaler Dreisatz bezeichnet. Es gilt: Je mehr, desto mehr. Beispiel: Je mehr Bananen ich kaufe, desto mehr muss ich bezahlen.
- Ungerader Dreisatz: Wird auch als antiproportionaler Dreisatz bezeichnet. Es gilt: Je mehr, desto weniger. Beispiel: Je mehr Handwerker arbeiten, desto schneller ist die Arbeit erledigt.
Beispiel proportional:
Stell dir vor, du gehst einkaufen. Dabei siehst du, dass eine Tafel Schokolade 1 Euro kostet. Wenn du zwei Tafeln Schokolade kaufst, kostet es dich 2 Euro. Drei Tafeln Schokolade kosten 3 Euro und so weiter. Dabei gibt es keinen Mengenrabatt in diesem Beispiel. Für jede weitere Tafel Schokolade zahlst du einen Euro mehr.
So etwas nennt man eine proportionale Zuordnung: Doppelte Menge, doppelter Preis. Dreifache Menge, dreifacher Preis und so weiter. Die Formel für eine solche lineare Gleichung lautet:
[y = k cdot x]Solche proportionalen Aufgaben lassen sich mit einem geraden Dreisatz rechnen. Dabei sind die Zahlen oft etwas komplizierter. Außerdem erfährt man meistens nicht, was ein Stück kostet, sondern was eine größere Anzahl kostet.
Beispiel gerader (= proportionaler) Dreisatz:
Nehmen wir als Beispiel ein Rezept für einen Kuchen, das für 4 Personen ausgelegt ist. In der Anleitung steht, dass bei 4 Personen 500 Gramm Mehl benötigt werden. Du möchtest jedoch mehr Kuchen machen, damit er für 7 Personen reicht. Wie viel Mehl benötigst du jetzt?
Lösung:
Der Dreisatz funktioniert so, dass man in die erste Zeile die vorhandenen Informationen einträgt. In diesem Fall sind es 4 Personen und 500 Gramm Mehl.
Anschließend rechnet man diese Informationen auf eine Person herunter. Dazu teilen wir hier beide Angaben durch 4. Bei 500 Gramm geteilt durch 4 kommen wir auf 125 Gramm.
Wir wissen jetzt, dass wir für eine Person 125 Gramm Mehl brauchen. Nun multiplizieren wir diese Menge mit 7, um auf 7 Personen zu kommen. Das ergibt 875 Gramm Mehl.
Mit diesem Dreisatz haben wir berechnet, dass wir 875 Gramm Mehl für 7 Personen benötigen.
Formel proportionaler Dreisatz
Diese Formel bzw. Vorgehensweise kann allgemein für den geraden Dreisatz angewendet werden. Hier ist noch einmal der vollständige Dreisatz mit farblicher Markierung und im Anschluss die Kurzberechnung mit Formel.
Mit der Formel zum Dreisatz sieht das folgendermaßen aus:
Der Dreisatz hat seinen Namen von den drei Zeilen, die dabei verwendet werden:
- Grundwert (G): Die Ausgangsinformationen
- Proportionaler Wert (P): Der Wert, der sich verändert, je nachdem wieviel Grundwert vorhanden ist
- Einheit (E): Die Maßeinheit, in der der proportionale Wert angegeben ist
Antiproportionalen Dreisatz erkennen und Beispiel
Bei den proportionalen Zuordnungen ging es immer nach dem Motto “Je mehr, desto mehr”. Doch das ist nicht immer so. Es gibt auch antiproportionale Zuordnungen bzw. Zusammenhänge. Hier gilt das Motto “Je mehr, desto weniger”.
Antiproportionalen Dreisatz erkennen:
Stell dir vor, eine Lagerhalle wurde bei einem Hochwasser überflutet. Die Feuerwehr beginnt damit, Pumpen aufzubauen, um das Wasser aus der Halle zu entfernen. Der Verantwortliche schätzt, dass man mit 2 Pumpen die Halle in 3 Tagen wasserfrei bekommen könnte. Der Betreiber der Lagerhalle möchte dies jedoch schneller erledigen und hätte gerne in einem halben Tag (0,5 Tage) die Lagerhalle wieder wasserfrei.
Der logische Verstand sagt bereits, dass mehr Pumpen die Lagerhalle schneller vom Wasser befreien können als weniger Pumpen. Hier gilt “Je mehr Pumpen, desto weniger Zeit”. Proportionale Aufgaben lösen wir mit dem geraden Dreisatz und antiproportionale Aufgaben mit dem ungeraden Dreisatz.
Beispiel ungerader (= antiproportionaler) Dreisatz:
Nehmen wir das Beispiel von eben: 2 Pumpen benötigen 3 Tage, um eine Lagerhalle von Wasser zu befreien. Wie viele Pumpen werden benötigt, um es in 12 Stunden zu schaffen?
Lösung: Wie auch beim geraden Dreisatz schreiben wir in die erste Zeile die Ausgangsinformationen: In 3 Tagen schaffen es 2 Pumpen.
Um von 3 Tagen auf 1 Tag zu kommen, teilen wir auf der linken Seite durch 3. Bei proportionalen Aufgaben würden wir auf der rechten Seite dasselbe tun. Doch hier haben wir eine antiproportionale Zuordnung. Daher multiplizieren wir auf der rechten Seite nicht durch 3, sondern mit 3. So kommen wir zu dem Ergebnis, dass 6 Pumpen die Lagerhalle an einem einzigen Tag wasserfrei pumpen könnten.
Nun interessiert uns bei dieser Aufgabenstellung, wie viele Pumpen man bräuchte, um alles in einem halben Tag (12 Stunden) zu schaffen. Um von einem ganzen Tag auf einen halben Tag zu kommen, teilen wir noch einmal durch 2. Und auch hier gilt: Es handelt sich um einen antiproportionalen Dreisatz. Daher multiplizieren wir auf der rechten Seite nicht durch 2, sondern mit 2.
Die Antwort: Mit 12 Pumpen schafft man es, die Lagerhalle in einem halben Tag von Wasser zu befreien (abgesehen von Restfeuchtigkeit).
Aufgaben / Übungen zum Dreisatz
Du hast 0 von 5 Aufgaben erfolgreich gelöst.