Der Logarithmus ist eine wichtige Rechenoperation, mit der wir den Exponenten einer bestimmten Zahl bestimmen können. Es ist die Umkehrung der Potenzierung. Um das Konzept des Logarithmus besser zu verstehen, betrachten wir ein einfaches Beispiel:
Angenommen, wir haben die Gleichung $2^x = 16$. Wir wissen, dass $2^4 = 16$ ist, aber wir möchten den Exponenten $x$ bestimmen, der diese Gleichung erfüllt. Genau hier kommt der Logarithmus ins Spiel.
Der Logarithmus beantwortet die Frage: “Mit welcher Zahl müssen wir $2$ potenzieren, um $16$ zu erhalten?” Die Lösung dieser Gleichung ist $x = log_2{16}$.
Allgemein löst die Gleichung $a^x = b$ durch $x = log_a{b}$. Die rechte Seite der Gleichung wird als “Logarithmus zur Basis $a$ von $b$” bezeichnet.
Es ist wichtig zu beachten, dass die Basis des Logarithmus positiv sein muss, da die Potenz einer positiven Zahl immer positiv ist.
Spezielle Logarithmen
Es gibt verschiedene Arten von Logarithmen, die häufig verwendet werden und eine spezielle Schreibweise haben:
- Der Logarithmus zur Basis $10$ wird als “dekadischer Logarithmus” bezeichnet und wird abgekürzt als $log_{10} = lg$ geschrieben.
- Der Logarithmus zur Basis $e$, der Euler’schen Zahl ($e approx 2,71828$), wird als “Logarithmus naturalis” bezeichnet: $log_e = ln$.
- Der Logarithmus zur Basis $2$ wird als “Logarithmus dualis” bezeichnet: $log_2 = ld$.
Die ersten beiden Logarithmen finden Sie auch auf Ihrem Taschenrechner. Die Schreibweise $ld$ wird nicht so häufig verwendet.
Schreibweise des Logarithmus
Die Schreibweise des Logarithmus kann auf den ersten Blick verwirrend sein. Es ist jedoch wichtig zu verstehen, wie der Logarithmus aufgebaut ist.
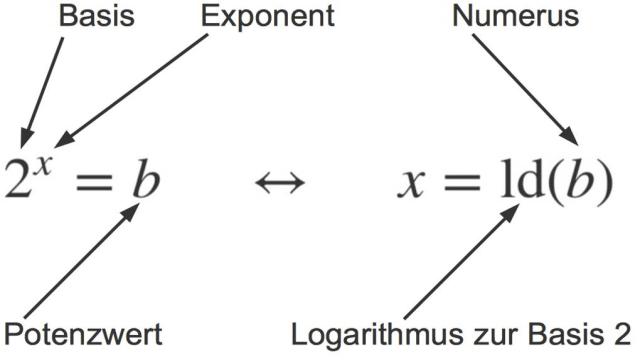
Hier ist der Zusammenhang zwischen Potenzierung (links) und Logarithmierung (rechts) am Beispiel des Logarithmus dualis und die entsprechenden Bezeichnungen:
- Die Basis der Potenz ist auch die Basis im Logarithmus. Statt $log_2$ können wir auch $ld$ schreiben.
- Der Exponent $x$ ist die gesuchte Zahl und steht isoliert auf der linken Seite der Logarithmus-Gleichung.
- Der Potenzwert $b$ wird zum Argument des Logarithmus und wird auch als “Numerus” bezeichnet.
Logarithmusgesetze
Die Logarithmusgesetze gelten für Logarithmen mit beliebigen Basen und auch für die oben genannten speziellen Logarithmen.
1. Logarithmusgesetz
Das 1. Logarithmusgesetz, auch als Produktregel bekannt, besagt, dass die Addition von Logarithmen mit der gleichen Basis das gleiche Ergebnis liefert:
$log_a(u cdot v) = log_a(u) + log_a(v)$
2. Logarithmusgesetz
Das 2. Logarithmusgesetz, auch als Quotientenregel bekannt, besagt, dass die Subtraktion von Logarithmen mit der gleichen Basis das gleiche Ergebnis liefert:
$log_aleft(frac{u}{v}right) = log_a(u) – log_a(v)$
3. Logarithmusgesetz
Das 3. Logarithmusgesetz, auch als Potenzregel bekannt, besagt, dass Potenzen in Logarithmen mit gleicher Basis multipliziert werden:
$log_a(u^r) = r cdot log_a(u)$
Dieses Gesetz gilt auch für Wurzeln, da Wurzeln als Potenz ausgedrückt werden können:
$log_a(sqrt[r]{u}) = frac{1}{r} cdot log_a(u)$
Basiswechsel
Wenn wir einen Logarithmus mit einer bestimmten Basis haben, können wir diesen Logarithmus in einen Logarithmus mit einer anderen Basis umwandeln. Ein Logarithmus zur Basis $a$ kann wie folgt in einen Logarithmus zur Basis $b$ umgewandelt werden:
$log_aP = frac{log_bP}{log_ba}$
Beispiel
Betrachten wir den Logarithmus: $log_39$.
Wir können die Basis dieses Logarithmus wie folgt in eine Basis $5$ umwandeln:
$log_39 = frac{log_59}{log_53}$
Aufgaben und Übungen zum Logarithmus
Einfache Exponentialgleichungen
Eine Gleichung, bei der die Unbekannte im Exponenten steht, wird als Exponentialgleichung bezeichnet. Mit Hilfe des Logarithmus können wir einige Exponentialgleichungen lösen, wenn wir die Potenzen umkehren. Hier sind einige Beispiele für Aufgaben zum Logarithmus:
- $log_3(9) = 2$, da $3^2 = 9$ ist.
- $log_5(125) = 3$, da $5^3 = 125$ ist.
- $log_7(2401) = 4$, da $7^4 = 2401$ ist.
Das Ergebnis kann auch negativ oder rational sein. Hier sind einige Beispiele:
- $0,5 = 2^{-1}$, daher ist $log_2(0,5) = -1$.
- $sqrt{3} = 3^{frac{1}{2}}$, daher ist $log_3(sqrt{3}) = frac{1}{2}$.
Lösen einer Exponentialgleichung
Für komplexere Fälle hilft uns der dekadische Logarithmus $lg$ weiter. Er kann auch dann helfen, wenn die Basis nicht $10$ ist. Betrachten wir das folgende Beispiel:
$3^x = 32$
Wir wenden den $lg$ auf beiden Seiten der Gleichung an:
$lg(3^x) = lg(32)$
Verwenden wir nun das 3. Logarithmusgesetz:
$x cdot lg(3) = lg(32)$
Durch Division beider Seiten durch $lg(3)$ erhalten wir die Lösung für die obige Gleichung:
$x = frac{lg(32)}{lg(3)} approx 3,155$
Dieser Trick mit dem dekadischen Logarithmus $lg$ ist sehr hilfreich, insbesondere wenn die Basis nicht $10$ ist.
Alltagsbeispiel
Paul legt $1000€$ zu einem jährlichen Zinssatz von $3,5%$ an. Mit Hilfe der Zinsrechnung können wir das Vermögen von Paul nach $n$ Jahren berechnen:
$K_n = 1000 cdot left(1 + frac{3,5}{100}right)^n = 1000 cdot 1,035^n$
Paul möchte nun wissen, wie lange er sein Kapital anlegen muss, um $1675€$ zu haben. Er muss die folgende Gleichung lösen:
$1675 = 1000 cdot 1,035^n$
Die unbekannte Größe steht im Exponenten. Um diese Gleichung zu lösen, benötigen wir den Logarithmus.
Wir teilen zunächst beide Seiten durch $1000$:
$1,675 = 1,035^n$
Dann wenden wir auf beiden Seiten den $lg$ an:
$lg(1,675) = lg(1,035^n)$
Verwenden wir nun das 3. Logarithmusgesetz:
$lg(1,675) = n cdot lg(1,035)$
Teilen wir nun beide Seiten durch $lg(1,035)$:
$n = frac{lg(1,675)}{lg(1,035)} approx 15$
Das bedeutet, dass Paul nach ungefähr $15$ Jahren ein Vermögen von $1675€$ hat.