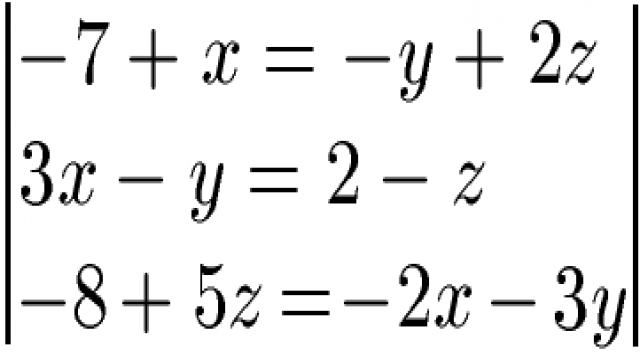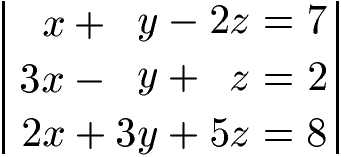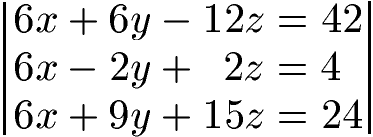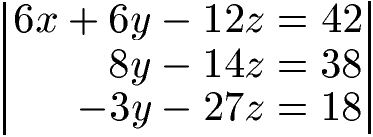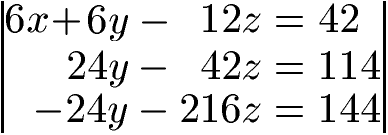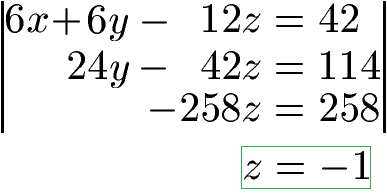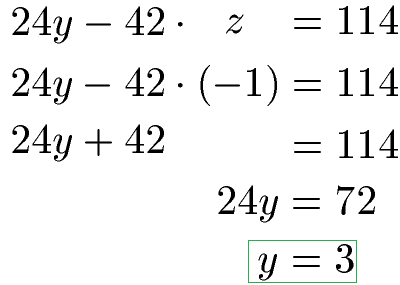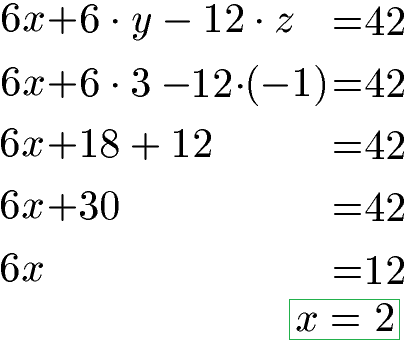Das Gauß-Verfahren, auch bekannt als Gauß-Algorithmus oder Gauß Eliminationsverfahren, ist eine Methode zur Lösung von linearen Gleichungssystemen. In diesem Artikel werden wir uns ansehen, wie man das Gauß-Verfahren verwendet und wie man damit Gleichungssysteme löst. Außerdem werden wir Übungen zur Verfügung stellen, damit du das Gelernte praktisch anwenden kannst.
Gauß Eliminationsverfahren einfach erklärt
Das Gauß-Verfahren wird zur Lösung von Gleichungssystemen verwendet, bei denen mehrere Gleichungen mit mehreren Variablen auftreten. Das Ziel des Verfahrens ist es, ein Gleichungssystem zu erstellen, bei dem in der ersten Zeile alle Variablen vorhanden sind und in den folgenden Zeilen jeweils eine Variable eliminiert wurde. Die Schritte des Verfahrens sind wie folgt:
- Bringe alle Terme mit Variablen auf eine Seite der Gleichung und die reinen Zahlen auf die andere Seite.
- Stelle sicher, dass die gleichen Variablen in allen Gleichungen untereinander angeordnet sind.
- Multipliziere oder dividieren bestimmte Gleichungen, um gleiche Faktoren zu erzeugen (das Vorzeichen kann unterschiedlich sein).
- Addiere oder subtrahiere Gleichungen, um eine Variable zu eliminieren.
- Wiederhole die Schritte 3 und 4, bis nur noch eine Variable übrig bleibt, und berechne sie.
- Setze die berechneten Werte in die übrigen Gleichungen ein, um die verbleibenden Variablen zu berechnen.
Es ist wichtig zu beachten, dass die Schritte beim Gauß-Verfahren oft verkürzt werden können. Anfänger haben jedoch oft Schwierigkeiten, diese Verkürzungen zu verstehen. Jeder sollte daher selbst entscheiden, wie detailliert die Schritte zur Lösung sein sollten.
Um das Verfahren besser zu verstehen, sehen wir uns ein Beispiel an, das ausführlich berechnet und erklärt wird.
Beispiel: Gaußsches Eliminationsverfahren einfach erklärt
In diesem Beispiel betrachten wir ein lineares Gleichungssystem mit drei Gleichungen und drei Unbekannten. Wir werden das Gaußsche Eliminationsverfahren verwenden, um die Werte von x, y und z zu berechnen.
Zunächst bringen wir alle Variablen auf die linke Seite der Gleichungen und die reinen Zahlen auf die rechte Seite. Die Terme mit x, y und z sollen dabei untereinander stehen.
Als nächstes möchten wir x eliminieren. Dazu multiplizieren wir die erste Gleichung mit 6, die zweite Gleichung mit 2 und die dritte Gleichung mit 3, um gleiche Faktoren zu erzeugen.
Jetzt subtrahieren wir die Gleichungen:
- Aus der ersten Gleichung subtrahieren wir die zweite Gleichung. Dabei erhalten wir 6x – 6x = 0. Weiterhin 6y – (-2y) = 8y und -12z – 2z = -14z. Auf der rechten Seite der Gleichung erhalten wir 42 – 4 = 38.
- Aus der ersten Gleichung subtrahieren wir die dritte Gleichung. Dabei erhalten wir 6x – 6x = 0. Weiterhin 6y – 9y = -3y und -12z – 15z = -27z. Auf der rechten Seite der Gleichung erhalten wir 42 – 24 = 18.
Nun haben wir noch zwei Gleichungen mit zwei Unbekannten (y und z). Um y zu eliminieren, multiplizieren wir die mittlere Gleichung mit 3 und die unterste Gleichung mit 8.
Durch Addition der beiden Gleichungen erhalten wir 24y + (-24y) = 0 und -42z + (-216z) = -258z. Auf der rechten Seite der Gleichung erhalten wir 114 + 144 = 258.
Durch -258z = 258 erhalten wir z = -1 als Lösung. Setzen wir dies in die mittlere Gleichung (24y -42z = 114) ein, erhalten wir y = 3.
Nun setzen wir y und z in eine Gleichung mit allen Variablen ein, um x zu berechnen.
Die Lösung lautet: x = 2, y = 3 und z = -1.
Aufgaben / Übungen Gleichungssysteme
Du hast 0 von 7 Aufgaben erfolgreich gelöst.
Fazit
Das Gauß-Verfahren ist eine effektive Methode zur Lösung von linearen Gleichungssystemen. Mit den richtigen Schritten und etwas Übung kannst du komplexe Gleichungen schnell und einfach lösen. Probier es doch gleich selbst aus!