Möchtest du wissen, wie man eine Mittelsenkrechte, eine Winkelhalbierende und eine Seitenhalbierende konstruiert? Dann bist du hier genau richtig! In diesem Artikel erkläre ich dir Schritt für Schritt, wie du diese Konstruktionen durchführst.
Eine kurze Wiederholung zu Dreiecken
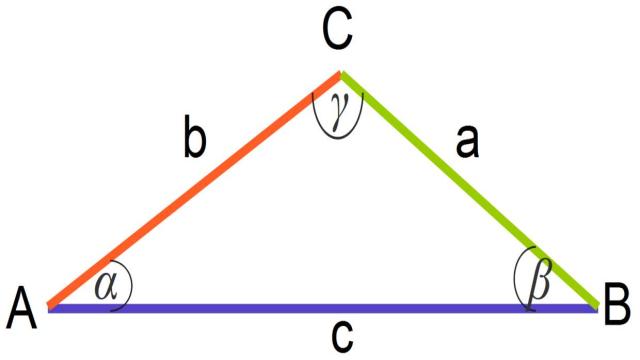
Bevor wir mit den Konstruktionen beginnen, wollen wir uns kurz mit Dreiecken vertraut machen. Ein Dreieck ist eine ebene Figur, die aus drei Ecken und drei Seiten besteht. Jeder Ecke ist ein Winkel zugeordnet, und die Summe der Winkel eines Dreiecks beträgt immer 180 Grad.
Was ist eine Mittelsenkrechte?
Eine Mittelsenkrechte ist eine Gerade, die senkrecht zu einer Strecke durch deren Mittelpunkt verläuft. Sie ist diejenige Gerade, auf der alle Punkte liegen, die den gleichen Abstand zu den beiden Endpunkten der Strecke haben.
Um eine Mittelsenkrechte zu konstruieren, folge diesen Schritten:
- Zeichne um jeden Endpunkt der Strecke einen Kreis mit dem gleichen Radius.
- Die beiden Kreise schneiden sich in zwei Punkten.
- Verbinde diese beiden Punkte miteinander, um die Mittelsenkrechte zu erhalten.
Was ist eine Winkelhalbierende?
Eine Winkelhalbierende ist ein Strahl, der von einem Scheitelpunkt eines Winkels ausgeht und den Winkel in zwei gleiche Teile teilt.
Um eine Winkelhalbierende zu konstruieren, gehe wie folgt vor:
- Zeichne um einen Eckpunkt des Winkels einen Kreis.
- Der Radius des Kreises muss kleiner sein als die kürzere der beiden Seitenlängen.
- Der Kreis schneidet jede der beiden Seiten des Winkels.
- Konstruiere den Mittelpunkt der Strecke zwischen den beiden Schnittpunkten.
- Verbinde den Scheitelpunkt des Winkels mit diesem Mittelpunkt, um die Winkelhalbierende zu erhalten.
Die Mittelsenkrechte, die Winkelhalbierende und die Seitenhalbierende schneiden sich jeweils in einem Punkt. Der Schnittpunkt der drei Mittelsenkrechten eines Dreiecks ist der Mittelpunkt des Umkreises, während der Schnittpunkt der drei Winkelhalbierenden der Mittelpunkt des Inkreises ist.
Ich hoffe, dieser Artikel hat dir geholfen, die Konstruktionen von Mittelsenkrechten, Winkelhalbierenden und Seitenhalbierenden besser zu verstehen. Wenn du weitere Fragen hast, stehe ich dir gerne zur Verfügung!