In diesem fantastischen Tutorial erfährst du alles, was du wissen musst, um die t-Verteilungstabelle zu lesen und richtig zu interpretieren. Schnapp dir ein Getränk und stell dich auf eins der aufregendsten Abenteuer in der Welt der Statistik ein!
Was ist die t-Verteilungstabelle?
Die t-Verteilungstabelle ist eine Schatzkarte, die uns die kritischen Werte der t-Verteilung zeigt. Um diese Tabelle richtig nutzen zu können, benötigst du nur drei wichtige Informationen:
- Die Freiheitsgrade des t-Tests
- Die Anzahl der Schwänze des T-Tests (einseitig oder zweiseitig)
- Das Alpha-Niveau des t-Tests (übliche Auswahlmöglichkeiten sind 0,01, 0,05 und 0,10)
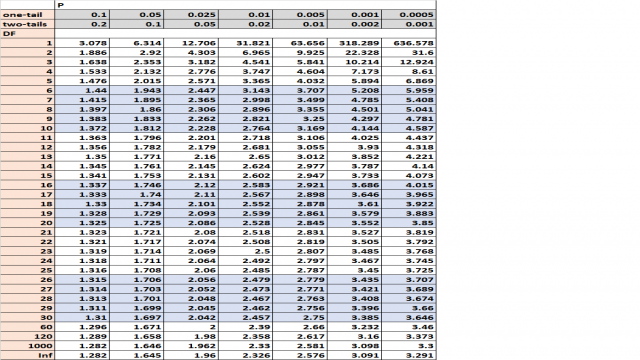
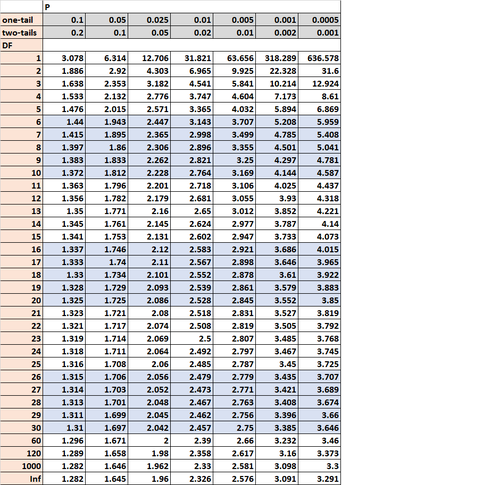
Schau dir dieses coole Beispiel einer t-Verteilungstabelle an, um einen Eindruck zu bekommen:
Stell dir vor, du führst einen t-Test durch. Du kannst die Teststatistik mit dem kritischen Wert aus der t-Verteilungstabelle vergleichen. Wenn die Teststatistik größer ist als der kritische Wert aus der Tabelle, kannst du die Nullhypothese des t-Tests ablehnen und daraus folgern, dass deine Ergebnisse statistisch signifikant sind.
Klingt spannend, oder? Lass uns nun einige Beispiele für die Verwendung der t-Distribution-Tabelle anschauen.
Beispiele für die Verwendung der t-Verteilungstabelle
In den folgenden Beispielen zeigen wir dir, wie du die t-Verteilungstabelle in verschiedenen Szenarien einsetzen kannst:
Beispiel 1: Einseitiger t-Test für einen Mittelwert
Stell dir vor, du führst einen einseitigen t-Test für einen Mittelwert mit einem Alpha-Level von 0,05 durch. Du hast 20 Probanden für deine Studie rekrutiert.
Frage: Wenn du deinen t-Test durchführst und eine Teststatistik t erhältst, mit welchem kritischen Wert solltest du t vergleichen?
Antwort: Bei einem t-Test mit einer Stichprobe sind die Freiheitsgrade gleich n-1, also in diesem Fall 20-1 = 19. Da du einen einseitigen Test durchführst und ein Alpha-Level von 0,05 verwendest, beträgt der entsprechende kritische Wert in der t-Verteilungstabelle 1,729.
Beispiel 2: Zweiseitiger t-Test für einen Mittelwert
Angenommen, du führst einen zweiseitigen t-Test für einen Mittelwert mit einem Alpha-Level von 0,10 durch. Du hast 18 Probanden für deine Studie rekrutiert.
Frage: Wenn du deinen t-Test durchführst und eine Teststatistik t erhältst, mit welchem kritischen Wert solltest du t vergleichen?
Antwort: Bei einem t-Test mit einer Stichprobe sind die Freiheitsgrade gleich n-1, also in diesem Fall 18-1 = 17. Da du einen zweiseitigen Test durchführst und ein Alpha-Level von 0,10 verwendest, beträgt der entsprechende kritische Wert in der t-Verteilungstabelle 1,74.
Beispiel 3: Bestimmen des kritischen Werts
Stell dir vor, du führst einen zweiseitigen t-Test für einen Mittelwert mit einer Stichprobengröße von 14 und einem Alpha-Level von 0,05 durch.
Frage: Wie hoch muss der absolute Wert deiner Teststatistik sein, um die Nullhypothese ablehnen zu können?
Antwort: Bei einem t-Test mit einer Stichprobe sind die Freiheitsgrade gleich n-1, also in diesem Fall 14-1 = 13. Da du einen zweiseitigen Test durchführst und ein Alpha-Level von 0,05 verwendest, beträgt der entsprechende kritische Wert in der t-Verteilungstabelle 2,16. Das bedeutet, dass du die Nullhypothese ablehnen kannst, wenn die Teststatistik t kleiner als -2,16 oder größer als 2,16 ist.
Beispiel 4: Vergleichen eines kritischen Werts mit einer Teststatistik
Angenommen, du führst einen rechtsseitigen t-Test für einen Mittelwert mit einer Stichprobengröße von 19 und einem Alpha-Level von 0,10 durch.
Frage: Deine Teststatistik t ergibt 1,48. Kannst du die Nullhypothese ablehnen?
Antwort: Bei einem t-Test mit einer Stichprobe sind die Freiheitsgrade gleich n-1, also in diesem Fall 19-1 = 18. Da du einen rechtsseitigen Test durchführst und ein Alpha-Level von 0,10 verwendest, beträgt der entsprechende kritische Wert in der t-Verteilungstabelle 1,33. Da deine Teststatistik t größer ist als 1,33, kannst du die Nullhypothese ablehnen.
Solltest du die t-Tabelle oder die z-Tabelle verwenden?
Manchmal kann es schwierig sein, zu entscheiden, welche Tabelle du verwenden solltest, um die kritischen Werte für ein bestimmtes Problem zu finden. Aber keine Sorge, wir haben für dich einen nützlichen Entscheidungsbaum:
Fazit
Herzlichen Glückwunsch, du bist jetzt ein wahrer Experte in der Kunst des Lesens der t-Verteilungstabelle! Mit diesem Wissen kannst du dich in der spannenden Welt der Statistik sicher bewegen. Wenn du noch mehr Informationen und Ressourcen suchst, empfehlen wir dir, eine vollständige Liste der Tabellen mit kritischen Werten zu erkunden, einschließlich einer Binomialverteilungstabelle, einer Chi-Quadrat-Verteilungstabelle und vielem mehr.
Jetzt kannst du stolz behaupten, dass du die Geheimnisse der t-Verteilungstabelle gelüftet hast. Beeindruckend, oder? Viel Spaß beim Anwenden dieses Wissens und beim Erobern neuer statistischer Herausforderungen!
Auf geht’s, Statistik-Heldin!