In diesem Artikel werden wir uns mit dem Thema Lineare Gleichungssysteme (LGS) beschäftigen. Wir erklären, was lineare Gleichungssysteme sind und wie man sie lösen kann. Außerdem gehen wir auf die verschiedenen Lösungsverfahren wie das Einsetzungsverfahren, das Gleichsetzungsverfahren und das Additionsverfahren ein. Und natürlich darf der Gauß-Algorithmus nicht fehlen. Also, lass uns loslegen!
Was sind lineare Gleichungssysteme (LGS)?
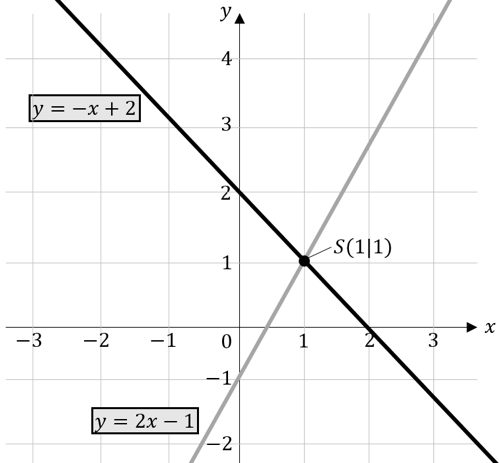
Bei linearen Gleichungssystemen handelt es sich um zwei oder mehr lineare Gleichungen mit mehreren Unbekannten. Die Lösung des Gleichungssystems sind die Werte, die sowohl alle Gleichungen erfüllen. Um dir das besser vorstellen zu können, betrachten wir ein Beispiel mit zwei linearen Gleichungen:
Gleichung I: $y=-x+2$
Gleichung II: $y=2x-1$
In diesem Fall sehen wir, dass die beiden Geraden sich im Punkt (1|1) schneiden. Die Steigungen der beiden Geraden sind unterschiedlich (-1 und 2). Das bedeutet, dass Geraden mit unterschiedlicher Steigung immer einen gemeinsamen Schnittpunkt haben. Geraden mit identischer Steigung verlaufen parallel oder sind sogar identisch, wenn sie auch den gleichen Schnittpunkt mit der y-Achse haben. Folgende Fälle werden unterschieden:
- $m_1 neq m_2$ ⇒ gemeinsamer Schnittpunkt
- $m_1 = m_2$ und $b_1 neq b_2$ ⇒ parallel
- $m_1 = m_2$ und $b_1 = b_2$ ⇒ identisch
($m_1$ = Steigung der ersten Geraden, $m_2$ = Steigung der zweiten Geraden, $b_1$ = Schnittpunkt der ersten Geraden mit der y-Achse, $b_2$ = Schnittpunkt der zweiten Geraden mit der y-Achse)
Von einer linearen Gleichung zum Gleichungssystem
Nun schauen wir uns an, wie man von einer einzelnen linearen Gleichung zu einem linearen Gleichungssystem kommt. Ein lineares Gleichungssystem enthält mehrere Unbekannte. Hier ein Beispiel:
$3x_1+4x_2=-1$
$2x_1+5x_2=3$
In diesem Fall haben wir zwei Gleichungen und zwei Unbekannte. Die Koeffizienten vor den Unbekannten werden zu den Koeffizienten der Gleichungen im linearen Gleichungssystem. Das Ziel besteht darin, die Werte der Unbekannten zu finden, die beide Gleichungen erfüllen.
LGS lösen mit Einsetzungsverfahren
Das Einsetzungsverfahren ist eine Möglichkeit, lineare Gleichungssysteme zu lösen. Dabei gehen wir wie folgt vor:
- Eine Gleichung nach einer Variablen auflösen.
- Den berechneten Ausdruck in die andere Gleichung einsetzen.
- Die so entstandene Gleichung nach der enthaltenen Variablen auflösen.
- Die Lösung in die ursprüngliche Gleichung einsetzen und die Variablen berechnen.
Beispiel für ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten:
$I: 2x_1 + 3x_2 = 12$
$II: x_1 – x_2 = 1$
Um das Einsetzungsverfahren anzuwenden, lösen wir zunächst Gleichung II nach $x_1$ auf:
$x_1 = x_2 + 1$
Nun setzen wir den Ausdruck für $x_1$ in Gleichung I ein:
$2(x_2 + 1) + 3x_2 = 12$
Diese Gleichung lösen wir nach $x_2$ auf:
$2x_2 + 2 + 3x_2 = 12$
$5x_2 + 2 = 12$
$5x_2 = 10$
$x_2 = 2$
Nun setzen wir $x_2 = 2$ in die umgeformte Gleichung $x_1 = x_2 + 1$ ein:
$x_1 = 2 + 1 = 3$
Die Lösung des Gleichungssystems ist also $x_1 = 3$ und $x_2 = 2$.
LGS lösen mit Gleichsetzungsverfahren
Das Gleichsetzungsverfahren ist eine weitere Methode, um lineare Gleichungssysteme zu lösen. Dabei gehen wir wie folgt vor:
- Beide Gleichungen nach derselben Variablen auflösen.
- Die beiden Seiten der Gleichungen gleichsetzen.
- Die so entstandene Gleichung nach der enthaltenen Variablen auflösen.
- Die Lösung in eine der umgeformten Gleichungen einsetzen und die Variablen berechnen.
Beispiel für ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten:
$I: 2x_1 + 3x_2 = 12$
$II: x_1 – x_2 = 1$
Um das Gleichsetzungsverfahren anzuwenden, formen wir beide Gleichungen nach $x_1$ um:
$Ia: x_1 = 6 – 1,5x_2$
$IIa: x_1 = x_2 + 1$
Nun setzen wir die beiden umgeformten Gleichungen gleich:
$6 – 1,5x_2 = x_2 + 1$
Diese Gleichung lösen wir nach $x_2$ auf:
$6 – 1,5x_2 = x_2 + 1$
$1,5x_2 + x_2 = 6 – 1$
$2,5x_2 = 5$
$x_2 = 2$
Abschließend setzen wir $x_2 = 2$ in eine der umgeformten Gleichungen (entweder $Ia$ oder $IIa$) ein, um $x_1$ zu berechnen:
$x_1 = 2 + 1 = 3$
Die Lösung des Gleichungssystems ist also $x_1 = 3$ und $x_2 = 2$.
Sonderfälle
Manchmal können sich die Geraden nicht schneiden, sondern parallel oder sogar identisch sein. In solchen Fällen erhalten wir natürlich keine Schnittpunktkoordinaten. Schauen wir uns dazu zwei Aufgaben an:
Parallele Geraden
Zwei parallele Geraden haben die gleiche Steigung, aber unterschiedliche Schnittpunkte mit der y-Achse. Betrachten wir das folgende lineare Gleichungssystem:
$I: y = 2x – 2$
$II: y = 2x – 5$
Wir sehen sofort, dass die Steigungen der beiden Geraden identisch sind. Allerdings haben sie unterschiedliche Schnittpunkte mit der y-Achse. Wenn wir das Gleichsetzungsverfahren anwenden, erhalten wir eine falsche Aussage:
$2x – 2 = 2x – 5$
$-2 = -5$
Da dies offensichtlich nicht stimmt, gibt es keine Lösung für das Gleichungssystem. Die beiden Geraden verlaufen also parallel zueinander.
Identische Geraden
Zwei identische Geraden sind nicht immer auf den ersten Blick erkennbar. Betrachten wir dazu das folgende Beispiel:
$I: 4x = 5 – y$
$II: 8x = 10 – 2y$
Auf den ersten Blick scheinen die Steigungen und die Schnittpunkte der beiden Geraden unterschiedliche Werte zu haben. Wenn wir jedoch das Gleichsetzungsverfahren anwenden wollen, teilen wir die zweite Gleichung durch 2:
$Ia: 4x = 5 – y$
$IIa: 4x = 5 – y$
Nun sehen wir, dass die beiden Gleichungen identisch sind. Wenn wir die Terme gleichsetzen und weiterrechnen, erhalten wir eine wahre Aussage:
$5 – y = 5 – y$
Da dies stimmt, sind die Geraden identisch.
LGS lösen mit Additionsverfahren
Das Additionsverfahren ist eine Methode, um lineare Gleichungssysteme zu lösen. Dabei gehen wir folgendermaßen vor:
- Entscheide, welche Unbekannte du eliminieren möchtest.
- Überlege, wie du vorgehen musst, um die Unbekannte zu eliminieren.
- Berechne die Unbekannten.
Beispiel für ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten:
$I: 2x_1 + 3x_2 = 12$
$II: x_1 – x_2 = 1$
Wir möchten $x_1$ eliminieren, indem wir $I – 2 cdot II$ rechnen:
$I: 2x_1 + 3x_2 = 12$
$II: x_1 – x_2 = 1$
$IIa: -2x_1 + 2x_2 = -2$
Nun können wir $x_2$ eliminieren, indem wir $I + 3 cdot II$ rechnen:
$I: 2x_1 + 3x_2 = 12$
$II: x_1 – x_2 = 1$
$IIb: 5x_2 = 10$
Die Lösung des Gleichungssystems ist also $x_1 = 3$ und $x_2 = 2$.
Gauß-Algorithmus
Der Gauß-Algorithmus ist eine Methode, um lineare Gleichungssysteme zu lösen. Dabei bringen wir das Gleichungssystem in eine spezielle Form, bei der unter der Hauptdiagonalen Nullen stehen. Das vereinfacht die Lösung des Gleichungssystems enorm.
Beispiel für ein Gleichungssystem mit drei Gleichungen und drei Unbekannten:
$1x_1 – 1x_2 + 2x_3 = 0$
$-2x_1 + 1x_2 – 6x_3 = 0$
$1x_1 – 2x_3 = 3$
Wir schreiben das Gleichungssystem in Matrixform:
$begin{array}{rrr|c}1 & -1 & 2 & 0 -2 & 1 & -6 & 0 1 & 0 & -2 & 3end{array}$
Unser Ziel ist es, unter der Hauptdiagonalen Nullen zu erzeugen:
$begin{array}{rrr|c}1 & -1 & 2 & 0 & -1 & -2 & 0 & 0 & -6 & 3end{array}$
Das Gleichungssystem lautet nun:
$1x_1 – 1x_2 + 2x_3 = 0$
$-x_2 – 2x_3 = 0$
$-6x_3 = 3$
Die Lösung des Gleichungssystems ist also $x_1 = 0$, $x_2 = 0$ und $x_3 = -frac{1}{2}$.
Das waren die Grundlagen zu linearen Gleichungssystemen. Wir hoffen, dass wir dir damit weiterhelfen konnten. Viel Erfolg beim Lösen von LGS!