Manchmal ist es etwas verwirrend, den Unterschied zwischen linearen und affinen Funktionen zu verstehen. Oft werden diese beiden Begriffe synonym verwendet. Jedoch sind sie streng genommen unterschiedlich. Linear muss affin sein, aber affin ist nicht zwangsläufig linear.
In diesem Artikel möchte ich den Unterschied und die Beziehung zwischen linearen und affinen Funktionen, Räumen und Transformationen diskutieren.
Lineare Funktion vs. Affine Funktion
Bei einem eindimensionalen System wurden lineare Funktionen oft als “y = ax + b” beschrieben. Doch das ist streng genommen eine affine Funktion. Eine lineare Funktion geht immer durch den Ursprung (0,0) und sollte folgendermaßen beschrieben werden: “y = ax”.
Um eine lineare Funktion zu bestimmen, benötigen wir nur einen Punkt (x1, y1) (da der andere Punkt immer (0, 0) ist). Um eine affine Funktion zu bestimmen, benötigen wir jedoch zwei Punkte (x1, y1) und (x2, y2).
Linearer Raum vs. Affiner Raum
Der lineare Raum wird auch als Vektorraum bezeichnet. Der Ursprung dieses Raums wird als 0 festgelegt und jeder Vektor im Vektorraum beginnt am Ursprung. Angenommen, v gehört zum Vektorraum V und w gehört zum Vektorraum V, dann haben wir: a*v gehört zu V, -v gehört zu V, v+w gehört zu V, 0 = v-v gehört zu V. Ein n-dimensionaler Vektorraum kann als lineare Kombination von n linear unabhängigen Vektoren beschrieben werden. Alternativ können auch n linear unabhängige Vektoren einen n-dimensionalen Vektorraum bestimmen. Zum Beispiel ist ein eindimensionaler Vektorraum eine Linie und ein zweidimensionaler Vektorraum eine Ebene.
Ein affiner Raum ist informell gesagt ein Vektorraum, dessen Ursprung nicht festgelegt ist. Angenommen, A ist ein affiner Raum und a ist ein Punkt in A und b ist ein Punkt in A, dann muss nicht unbedingt gelten: a+a’ ist in A, -a ist in A, a+b ist in A, 0 = a-a ist in A. Jeder affiner Raum hat einen zugehörigen Vektorraum V, sodass die Verschiebungsvektoren v = a-b zwischen zwei Punkten a in A und b in A aus dem affinen Raum A im zugehörigen Vektorraum V liegen. Die Dimension eines affinen Raums wird durch die Dimension seines zugehörigen Vektorraums bestimmt.
Formal betrachtet ist ein affiner Raum eine Menge A zusammen mit einem Vektorraum V und einer transitiven und freien Aktion der additiven Gruppe von V auf die Menge A. Diese Definition erzeugt eine Abbildung von A und V nach A:
A × V → A
(a, v) ↦ a + v
wobei a in A, v in V und ↦ tatsächlich eine Bijektion ist.
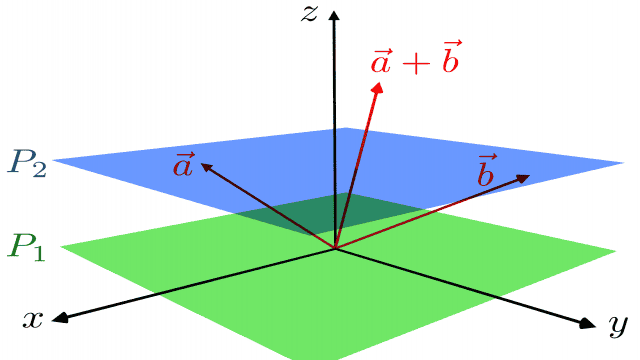
Im Folgenden finden Sie ein Beispiel für einen affinen Raum.
Der Punkt 0 gehört zu P1, aber P1 ist nicht unbedingt gleich z = 0. Die Punkte P1 und P2 sind parallel zueinander. Basierend auf der formalen Definition des affinen Raums können wir erkennen, dass P2 ein affiner Raum ist und P1 der Vektorraum ist, der mit dem affinen Raum P2 assoziiert ist. Speziell gehört a zu P2 und b zu P2, a+b nicht zu P2, 0 nicht zu P2 und a-b gehört zu P1.
Angenommen, P1: {av + bw}, wobei v in R^3, w in R^3 und v ≠ kw. Da P1 zwei linear unabhängige Punkte hat, ist P1 ein 2-dimensionaler Vektorraum. Darüber hinaus gilt für P2: {av + bw + u}, wobei u ein Translationsvektor ist. Gegeben zwei Punkte im affinen Raum P2, a = a1v + b1w + u und b = a2v + b2w + u, haben wir a-b = (a1-a2)v + (b1-b2)w, und dies liegt im zugehörigen Vektorraum P1. Da der zugehörige Vektorraum P1 des affinen Raums P2 2-dimensional ist, ist der affine Raum P2 nach Definition 2-dimensional.
Die nächste Frage ist, wie viele affin unabhängige Punkte wir benötigen, um einen n-dimensionalen affinen Raum zu bestimmen. Beachten Sie in dem obigen Beispiel, dass zwei Punkte a und b nicht ausreichen, um den 2-dimensionalen affinen Raum zu bestimmen. Wenn wir jedoch einen dritten Punkt c haben und a-c in P1 liegt, b-c in P1 liegt und a-c und b-c linear unabhängig sind, können wir den 2-dimensionalen affinen Raum bestimmen. Daher benötigen wir zur Bestimmung eines n-dimensionalen affinen Raums n + 1 affin unabhängige Punkte. Hier ist eine Menge von n + 1 affin unabhängigen Punkten eine affine Basis des affinen Raums. Beachten Sie, dass wir hier nicht definiert haben, was eine affine Basis ist. Aber wir haben bereits ein gutes Gefühl dafür, dass {x0, …, xn} eine affine Basis eines affinen Raums ist, wenn {x1-x0, …, xn-x0} eine lineare Basis des zugehörigen Vektorraums ist.
Der Vektorraum ist auch ein affiner Raum. Der n-dimensionale Vektorraum hat eine Basis, die aus n linear unabhängigen Punkten {x1, …, xn} besteht, und hat n + 1 affin unabhängige Punkte {0, x1, …, xn}. Beachten Sie, dass der Ursprung 0 in einem affinen Raum, der auch ein Vektorraum ist, in der affinen Basis enthalten sein muss.
Lineare Transformation vs. Affine Transformation
Die lineare Funktion und die affine Funktion sind nur Spezialfälle der linearen Transformation und der affinen Transformation. Angenommen, wir haben einen Punkt x in R^n und eine quadratische Matrix M in R^(n x n). Die lineare Transformation von x mit M kann wie folgt beschrieben werden: y = Mx.
Angenommen, wir haben einen weiteren Translationsvektor b in R^n. Die affine Transformation von x mit M und b kann wie folgt beschrieben werden: y = Mx + b.
Eine affine Transformation in einem n-dimensionalen affinen Raum entspricht tatsächlich einer linearen Transformation in einem n + 1-dimensionalen Raum. Um dies zu sehen, erinnern wir uns an die erweiterten Koordinaten, die ich in meinem vorherigen Artikel “2D Line Mathematics Using Homogeneous Coordinates” erwähnt habe. Wir werden die erweiterten Koordinaten für x und y verwenden. Die oben beschriebene affine Transformation kann auch mit erweiterten Koordinaten beschrieben werden:
[ y | 1 ] = [ M b | 0 1 ] [ x | 1 ] = [ Mx + b | 1 ]Daher entspricht eine affine Transformation in einem n-dimensionalen affinen Raum tatsächlich einer linearen Transformation in einem n + 1-dimensionalen Raum.
Referenzen:
- Affine Space – Wikipedia
- What is… an Affine Space?
- What is… an Affine Map?