Die Vektorgeometrie beschäftigt sich mit den grundlegenden Konzepten von Punkten, Geraden und Ebenen. In diesem Artikel werden wir uns mit den verschiedenen Formen und Eigenschaften von Punkten, Geraden und Ebenen befassen. Wir werden lernen, wie man sie im dreidimensionalen Koordinatensystem zeichnet und wie man ihre Parameter- und Koordinatenformen umwandelt.
Zeichnen im 3D-Koordinatensystem
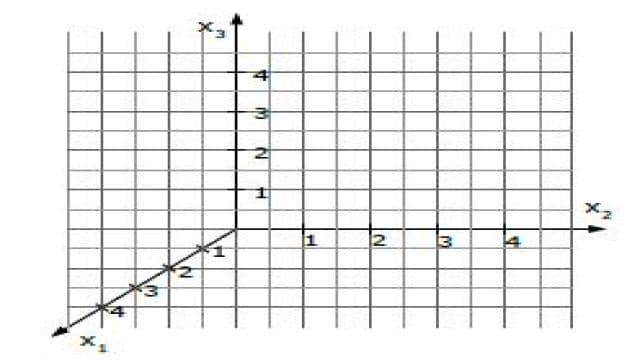
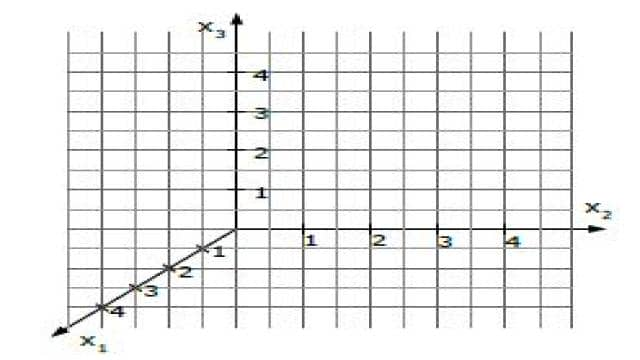
Ein dreidimensionales Koordinatensystem besteht aus drei Achsen: x1, x2 und x3. Die x1-Achse zeigt nach vorne, die x2-Achse nach rechts und die x3-Achse nach oben. Jede Achse hat ihre eigene Einheit und Richtung.
Punkte einzeichnen
Um einen Punkt in das 3D-Koordinatensystem einzutragen, beginnen wir im Ursprung und gehen dann entlang der x1-, x2- und x3-Achse. Die Koordinaten des Punktes geben an, wie weit wir in jede Richtung gehen müssen.
Beispiel:
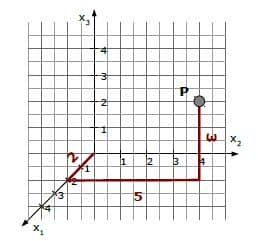
Lassen Sie uns den Punkt P(2|5|3) einzeichnen. Wir beginnen im Ursprung, gehen 2 Einheiten in Richtung x1, dann 5 Einheiten in Richtung x2 und schließlich 3 Einheiten in Richtung x3. Der Punkt P(2|5|3) ist erreicht.
Geraden einzeichnen
Um eine Gerade einzutragen, beginnen wir mit einem sogenannten Stützvektor, der den Ausgangspunkt der Gerade darstellt. Anschließend zeichnen wir den Richtungsvektor ein und verbinden die beiden Punkte.
Beispiel:
Lassen Sie uns die Gerade g mit den Punkten P(2|3|4) und Q(5|7|10) einzeichnen.
Lösung:
Um die