In der Mathematik gibt es zwei wichtige Konzepte, die uns helfen, Wahrscheinlichkeiten zu verstehen: die absolute Häufigkeit und die relative Häufigkeit. In diesem Artikel werden wir uns mit diesen Begriffen genauer befassen und sehen, wie sie in der Wahrscheinlichkeitsrechnung Anwendung finden.
Begriff Wahrscheinlichkeit
Wahrscheinlichkeit ist ein Begriff, den wir im Alltag oft verwenden, wenn wir etwas vermuten oder erwarten. In der Mathematik wird dieser Begriff jedoch präziser definiert. Hier untersucht man Vorgänge, die zufällig ablaufen und mehrere mögliche Ergebnisse haben können. Ein klassisches Beispiel ist das Würfeln. Die Augenzahlen 1, 2, 3, 4, 5 und 6 sind die möglichen Ergebnisse, von denen eines zufällig eintritt.
Begriff Zufallsexperiment
Ein Zufallsexperiment ist ein Vorgang mit zufälligem Ausgang, der unter genau festgelegten Bedingungen durchgeführt wird. Wenn solche Experimente unter immer gleichen Bedingungen wiederholt werden, können wir Aussagen über die Häufigkeiten bestimmter Ergebnisse oder Ereignisse treffen.
Absolute Häufigkeit und relative Häufigkeit
Die absolute Häufigkeit eines Ereignisses ist die genaue Anzahl, wie oft dieses Ereignis in einem Experiment auftritt. Die relative Häufigkeit hingegen ist das Verhältnis der absoluten Häufigkeit zur Gesamtanzahl der Durchführungen des Experiments.
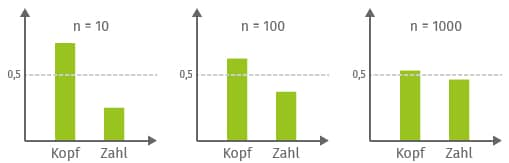
Ein Beispiel zur Veranschaulichung sind Verkehrsbeobachtungen. Wenn wir das Experiment mehrmals durchführen und die Ergebnisse in einem Diagramm darstellen, werden wir feststellen, dass die relativen Häufigkeiten um einen bestimmten Wert schwanken. Je häufiger das Experiment wiederholt wird, desto genauer stimmen die relative Häufigkeit und die Wahrscheinlichkeit überein. Dieses Phänomen wird als Gesetz der großen Zahlen bezeichnet.
Laplace-Experimente
Münzwurf und Würfeln sind Beispiele für eine bestimmte Art von Zufallsexperimenten, die als Laplace-Experimente bezeichnet werden. Bei diesen Experimenten ist jeder Versuchsausgang gleich wahrscheinlich. Wenn es beispielsweise a mögliche Ergebnisse gibt, ist die Wahrscheinlichkeit für jedes einzelne Ergebnis p = 1/a.
Darstellung im Baumdiagramm
Die Ergebnismenge eines mehrstufigen Zufallsexperiments kann in einem Baumdiagramm dargestellt werden. Auf jeder Stufe des Diagramms verzweigt es sich entsprechend den möglichen Ergebnissen. Die Wahrscheinlichkeiten für bestimmte Ereignisse werden entlang der einzelnen Pfade des Baumdiagramms eingetragen.
Ein anschauliches Beispiel für ein Laplace-Experiment ist das Ziehen von Losen aus einer Lostrommel. In einem Baumdiagramm können wir die möglichen Ergebnisse und die dazugehörigen Wahrscheinlichkeiten abbilden.
Pfadregeln: Produktregel und Summenregel
Für die Wahrscheinlichkeiten in einem mehrstufigen Zufallsexperiment oder im zugehörigen Baumdiagramm gelten zwei wichtige Pfadregeln: die Produktregel und die Summenregel.
Die Produktregel besagt, dass die Wahrscheinlichkeit entlang eines Pfades im Baumdiagramm gleich dem Produkt der Einzelwahrscheinlichkeiten entlang dieses Pfades ist. Die Summenregel besagt, dass die Wahrscheinlichkeit eines Ereignisses die Summe der Wahrscheinlichkeiten der Pfade ist, die zu diesem Ereignis gehören.
Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, müssen wir also diese beiden Regeln anwenden.
Insgesamt helfen uns die Begriffe der absoluten und relativen Häufigkeit sowie die Konzepte der Laplace-Experimente und des Baumdiagramms, die Wahrscheinlichkeit von Ereignissen zu verstehen und zu berechnen. Je öfter wir ein Experiment wiederholen, desto näher kommen die relativen Häufigkeiten den theoretischen Wahrscheinlichkeiten. So können wir experimentell die Wahrscheinlichkeit eines Ereignisses ermitteln und die Grundlagen der Wahrscheinlichkeitsrechnung besser verstehen.