Ein rechtwinkliges Dreieck ist ein besonderes Dreieck, das einen Winkel von 90 Grad aufweist. In diesem Artikel werden die trigonometrischen Funktionen Sinus, Cosinus und Tangens erklärt, die verwendet werden, um die Winkel und Seitenlängen rechtwinkliger Dreiecke zu berechnen.
Was ist ein rechtwinkliges Dreieck?
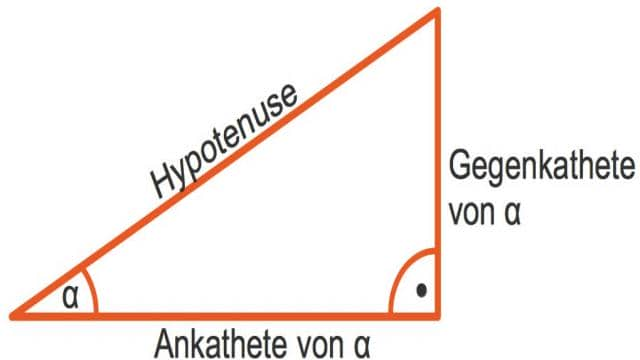
Ein rechtwinkliges Dreieck hat einen rechten Winkel, also einen Winkel von 90 Grad. Die längste Seite des Dreiecks wird als Hypotenuse bezeichnet, während die beiden anderen Seiten die Katheten sind. Die Kathete, die dem Winkel gegenüberliegt, wird als Gegenkathete bezeichnet, während die Kathete, die dem Winkel anliegt, als Ankathete bezeichnet wird.
Wie sind der Sinus, Cosinus und Tangens definiert?
Der Sinus
Der Sinus eines spitzen Winkels in einem rechtwinkligen Dreieck ist definiert als das Verhältnis der Länge der Gegenkathete zu der Länge der Hypotenuse:
sin(alpha) = Gegenkathete von alpha / Hypotenuse
Der Kosinus
Der Kosinus eines spitzen Winkels ist definiert als das Verhältnis der Länge der Ankathete zu der Länge der Hypotenuse:
cos(alpha) = Ankathete von alpha / Hypotenuse
Der Tangens
Der Tangens eines spitzen Winkels ist definiert als das Verhältnis der Länge der Gegenkathete zu der Länge der Ankathete:
tan(alpha) = Gegenkathete von alpha / Ankathete von alpha
Die trigonometrischen Funktionen Sinus, Cosinus und Tangens werden auch als trigonometrische Funktionen bezeichnet.
Anwendung des Sinus, Cosinus und Tangens
Im Folgenden werden einige Anwendungen der trigonometrischen Funktionen beschrieben.
Paul am Fluss
Paul möchte wissen, wie weit er über die Brücke und entlang des Flusses gehen muss, um zu seinem Freund Luke zu gelangen. Er kennt die Länge der Brücke und die Entfernung entlang des Flussufers. Indem er den Kosinus verwendet, kann er die Länge des Weges berechnen.
Der Flächeninhalt eines Drachenvierecks
Paul und Luke möchten einen Drachen steigen lassen und möchten die Fläche des Drachens berechnen. Indem Paul den Tangens verwendet, kann er die fehlende Höhe des Drachens bestimmen und somit die Fläche berechnen.
Der trigonometrische Pythagoras
Der trigonometrische Pythagoras besagt, dass die Summe der Quadrate der Sinus- und Kosinuswerte eines Winkels immer 1 ergibt. Dieser Zusammenhang kann am Einheitskreis verdeutlicht werden.
Diese Beispiele verdeutlichen, wie wichtig es ist, die trigonometrischen Funktionen zu verstehen und anzuwenden, um Winkel und Seitenlängen rechtwinkliger Dreiecke zu berechnen. Mit diesem Wissen kannst du komplexe geometrische Probleme lösen und beeindruckende mathematische Leistungen erbringen!