Willkommen zu unserem kleinen Geheimtipp: der Trigonometrie! Du denkst vielleicht, dass diese mathematische Disziplin schwierig ist, aber sie ist eigentlich ganz einfach und kann dir helfen, unbekannte Winkel oder Seitenlängen in rechtwinkligen Dreiecken zu berechnen. In diesem Artikel werde ich dir die Grundlagen von Sinus, Kosinus und Tangens erklären und dir zeigen, wie du sie anwenden kannst. Lass uns loslegen!
Grundbegriffe
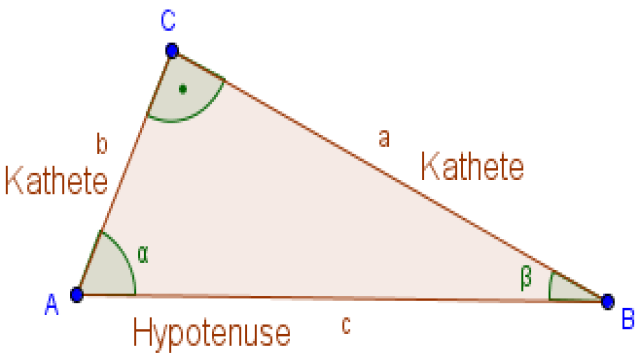
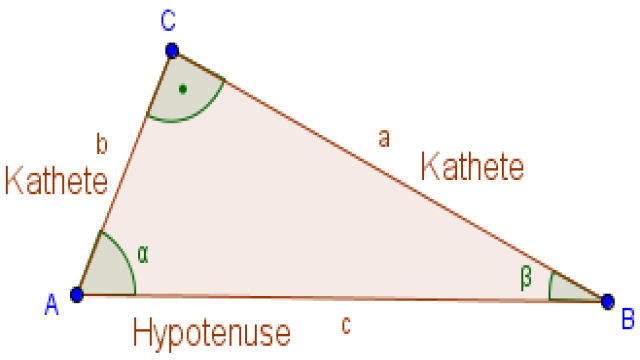
In einem rechtwinkligen Dreieck gibt es immer eine lange Seite, die gegenüber vom rechten Winkel liegt und Hypotenuse genannt wird. Die beiden kürzeren Seiten werden Katheten genannt. Die Hypotenuse wird oft mit dem Buchstaben c bezeichnet, während die Katheten mit a und b gekennzeichnet werden. Die Winkel in einem rechtwinkligen Dreieck werden üblicherweise mit α und β bezeichnet. Der rechte Winkel benötigt keine spezielle Bezeichnung. Hier ist eine grafische Darstellung:
Sinus, Kosinus, Tangens erklärt
Jetzt fragst du dich vielleicht, wie man Sinus, Kosinus und Tangens verwendet, um Winkel oder Seitenlängen zu berechnen. Keine Sorge, es ist gar nicht so kompliziert, wie es klingt. Schauen wir uns ein paar Beispiele an:
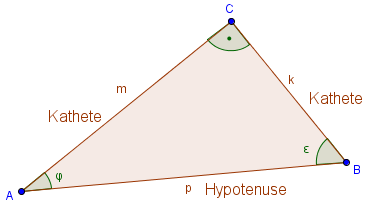
Angenommen, wir möchten den Sinus des Winkels φ berechnen. Wir suchen also den Winkel im Dreieck, der sich unten links befindet. Der Sinus ist definiert als das Verhältnis der Gegenkathete zur Hypotenuse. In diesem Fall ist die Hypotenuse p, da sie die längste Seite ist und dem rechten Winkel gegenüber liegt. Die Gegenkathete ist k, da sie der Kathete ist, die φ gegenüber liegt. Also gilt:
sin φ = Gegenkathete / Hypotenuse = k / pAuf ähnliche Weise können wir den Kosinus des Winkels ε berechnen. Der Kosinus ist das Verhältnis der Ankathete zur Hypotenuse. Also:
cos ε = Ankathete / Hypotenuse = k / pUnd schließlich gibt es noch den Tangens des Winkels φ. Hier teilen wir die Gegenkathete durch die Ankathete:
tan φ = Gegenkathete / Ankathete = k / mFazit
Diese Grundlagen gelten immer und können dir helfen, rechtwinklige Dreiecke zu berechnen. Mit Sinus, Kosinus und Tangens kannst du Winkel und Seitenlängen bestimmen. Also lass dich nicht von den mathematischen Begriffen abschrecken – die Trigonometrie ist ein nützliches Werkzeug, das dir in vielen Alltagssituationen helfen kann. Viel Spaß beim Ausprobieren!
Und falls du noch weitere Fragen hast, schau doch mal in unseren Abschnitt mit interessanten Fragen und Antworten zu Sinus, Kosinus und Tangens rein!
Interessante Fragen und Antworten zu Trigonometrie
Was genau rechnet man mit Sinus, Cosinus und Tangens aus?
Mit Sinus, Cosinus und Tangens kannst du die Winkel und Seitenlängen eines rechtwinkligen Dreiecks berechnen. Ein rechtwinkliges Dreieck hat einen rechten Winkel und die Seiten werden als Gegenkathete, Ankathete und Hypotenuse bezeichnet.
Was haben Sinus, Cosinus und Tangens mit Winkeln zu tun?
Sinus, Cosinus und Tangens beschreiben das Verhältnis von Seitenlängen in einem rechtwinkligen Dreieck. Sie werden daher auch als Winkelfunktionen bezeichnet. Sinus beschreibt das Verhältnis von Gegenkathete zu Hypotenuse, Cosinus das Verhältnis von Ankathete zu Hypotenuse und Tangens das Verhältnis von Gegenkathete zu Ankathete.
Was unterscheidet Sinus, Cosinus und Tangens?
Sinus, Cosinus und Tangens sind trigonometrische Funktionen zur Berechnung von Winkeln in einem rechtwinkligen Dreieck. Sie unterscheiden sich in der Art der Berechnung, da Sinus das Verhältnis von Gegenkathete zu Hypotenuse ist, Cosinus das Verhältnis von Ankathete zu Hypotenuse und Tangens das Verhältnis von Gegenkathete zu Ankathete.
Wie berechne ich den Cosinus Alpha, wenn ich den Sinus Alpha gegeben habe?
Der Cosinus Alpha kann berechnet werden, indem der Sinus Alpha verwendet wird. Dabei wird der Zusammenhang Sinus Alpha^2 + Cosinus Alpha^2 = 1 genutzt. Durch Umstellen dieser Gleichung erhält man den Cosinus Alpha.
Wie finde ich aus dem Tangens den Cosinus und den Sinus?
Um den Cosinus und den Sinus aus dem Tangens zu berechnen, benötigt man zusätzliche Informationen über die Seitenlängen des Dreiecks. Da der Tangens das Verhältnis von Gegenkathete zu Ankathete ist, kann man mit diesem Wissen die Hypotenuse berechnen. Mit der Hypotenuse können dann der Cosinus und der Sinus bestimmt werden.
Wo liegen die Nullstellen von Sinus und Cosinus und wie finde ich sie?
Die Nullstellen von Sinus und Cosinus liegen bei bestimmten Winkeln im Bereich von 0° bis 90°. Um die Nullstellen zu finden, muss man die trigonometrischen Gleichungen verwenden und passende Werte für die Winkel einsetzen. Es ist wichtig, die richtigen Zahlen einzusetzen, um genaue Ergebnisse zu erhalten. Die Berechnung der Nullstellen ist eine grundlegende Fähigkeit in der Mathematik und kann in vielen Bereichen von Bedeutung sein.