Wenn du dich jemals mit Trigonometrie beschäftigt hast, bist du wahrscheinlich auf Gleichungen gestoßen, die Sinus, Cosinus oder Tangens enthalten. Das Lösen solcher Gleichungen kann eine Herausforderung sein, aber keine Sorge, ich werde dir einige hilfreiche Tipps geben.
Was ist eine trigonometrische Gleichung?
Eine trigonometrische Gleichung ist eine Gleichung, in der mindestens eine trigonometrische Funktion vorkommt. Das können Sinus, Cosinus oder Tangens sein. Um solche Gleichungen zu lösen, benötigst du einen Taschenrechner, der auf Gradmaß eingestellt ist.
Lösen von trigonometrischen Gleichungen
Sinus: sin(x) = c
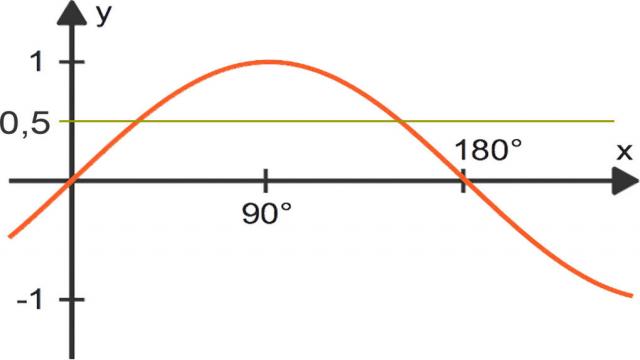
Um eine Gleichung wie sin(x) = 0,5 zu lösen, kannst du den Arkussinus (sin^-1 oder arcsin) auf deinem Taschenrechner verwenden. Eine Lösung dieser Gleichung ist x1 = sin^-1(0,5) = 30°. Da die Sinusfunktion periodisch ist, gibt es eine weitere Lösung: x2 = 180° – 30° = 150°. Die Lösungen können allgemein dargestellt werden als x1^(k) = 30° + k 360° und x2^(k) = 150° + k 360°.
Cosinus: cos(x) = c
Bei Gleichungen der Form cos(x) = c kannst du den Arkuskosinus (cos^-1 oder arccos) verwenden. Der Taschenrechner gibt Werte zwischen 0° und 180° aus. Die andere Basislösung erhältst du, indem du das Vorzeichen änderst. Auch hier ist die Periodizität der Cosinusfunktion wichtig. Zum Beispiel ist die Lösung für cos(x) = 1/sqrt(2) gegeben durch x1 = arccos(1/sqrt(2)) = 45°. Die Lösungsgesamtheit lautet x1^(k) = 45° + k 360° und x2^(k) = -45° + k 360°.
Tangens: tan(x) = c
Die Tangensfunktion ist 180°-periodisch und nicht definiert für 90° und -90°. Der Taschenrechner gibt Winkel zwischen -90° und 90° aus. Zum Beispiel ist die Lösung für tan(x) = 1 gleich x = arctan(1) = 45°. Die Lösungsgesamtheit ist x^(k) = 45° + k * 180°.
Trigonometrische Gleichungen mit zwei Winkelfunktionen
Manchmal tauchen in einer Gleichung zwei verschiedene Winkelfunktionen mit demselben Argument auf. In diesem Fall kannst du die Faktoren getrennt betrachten und jeweils die Lösungen bestimmen.
Trigonometrische Gleichungen mit zwei Winkelfunktionen und unterschiedlichen Argumenten
In solchen Gleichungen kommen verschiedene Winkelfunktionen mit unterschiedlichen Argumenten vor. Du kannst eine Substitution vornehmen, um die Gleichung auf eine quadratische Funktion zu reduzieren. Anschließend kannst du die p-q-Formel verwenden, um die Lösungen zu berechnen.
Jetzt hast du einen Überblick über das Lösen von trigonometrischen Gleichungen. Probiere es aus und finde die Lösungen zu übungszwecken!