Verständnis der Algebra: Warum faktorisieren wir Gleichungen?

Was geht eigentlich in der Algebra vor sich? Wenn man sich Variablen (x, y, z) ansieht, scheinen sie eine Zahl zu “verbergen”:

Welche Zahl könnte sich in x “verstecken”? In diesem Fall 2.

Es scheint, dass die Arithmetik immer noch funktioniert, selbst wenn wir die genauen Zahlen nicht haben. Später könnten wir diese “versteckten Zahlen” auf komplexe Weise anordnen:

Wow – etwas schwieriger zu lösen, aber es ist möglich. Heute wollen wir herausfinden, wie das Faktorisieren funktioniert und warum es nützlich ist.

Polynome

Wenn wir ein Polynom wie x^2 + x = 6 schreiben, können wir auf einer höheren Ebene denken.

Wir haben eine unbekannte Zahl x, die mit sich selbst interagiert (x * x = x^2). Wir fügen die ursprüngliche Zahl hinzu (+ x) und das Ergebnis ist 6.

x^2, x und 6 sind allesamt “Zahlen”, aber jetzt halten wir fest, wie sie gemacht werden:

• x^2 ist eine Komponente, die mit sich selbst interagiert
• x ist eine eigenständige Komponente
• 6 ist der gewünschte Zustand, den wir für das gesamte System erreichen möchten

Nach Abschluss der Interaktionen sollten wir 6 erhalten. Welche Zahl könnte sich in x verbergen, um dies wahr zu machen?

Hm, das ist knifflig. Also kämpfen wir mit einem Trick: Wir können ein anderes System erstellen, um den Fehler in unserem ursprünglichen System zu verfolgen (das ist verwirrend, also haltet durch).

Unser ursprüngliches System ist x^2 + x. Der gewünschte Zustand ist 6. Ein neues System:

[ text{wird den Unterschied zwischen dem ursprünglichen System und dem gewünschten Zustand verfolgen. Wann sind wir am glücklichsten? Wenn es keinen Unterschied gibt:} ]

Ah! Deshalb interessieren wir uns so sehr dafür, Polynome auf null zu setzen! Wenn wir ein System und den gewünschten Zustand haben, können wir eine neue Gleichung erstellen, um den Unterschied zu verfolgen und versuchen, ihn auf null zu setzen. (Das geht tiefer als nur “6 von beiden Seiten subtrahieren” – wir versuchen den Fehler zu beschreiben!)

Aber wie bekommen wir den Fehler tatsächlich auf null? Es ist immer noch ein Durcheinander von Komponenten: x^2, x und 6 fliegen überall herum.

Das Faktorisieren

Faktorisieren to the rescue! Meine Intuition: Faktorisieren ermöglicht es uns, ein komplexes System (x^2 + x – 6) als eine Reihe von verbundenen, kleineren Systemen neu anzuordnen.

Stellt euch vor, ihr nehmt einen Haufen Stäbchen (unser unordentliches, unorganisiertes System) und stellt sie so auf, dass sie sich gegenseitig stützen, wie ein Tipi:

/

(Das ist ein 2D-Beispiel mit zwei Stäbchen).

Entfernt man ein Stäbchen, kollabiert die gesamte Struktur. Wenn wir unser System umschreiben können als:

[ text{haben wir die Stäbchen in einem “Tipi” platziert}. Wenn Komponente A oder Komponente B zu 0 wird, kollabiert die Struktur und wir erhalten 0 als Ergebnis.

Klasse! Das ist der Grund, warum das Faktorisieren so gut funktioniert: Wir ordnen unser Fehler-System zu einem zerbrechlichen Tipi um, so dass wir es brechen können. Wir werden herausfinden, was unsere Fehler auslöscht und unser System in den idealen Zustand bringt.

Denkt daran: Wir brechen den Fehler im System, nicht das System selbst.

Nun zum Faktorisieren

Das Erlernen des “Faktorisierens einer Gleichung” ist der Prozess, das Tipi zu arrangieren. In diesem Fall:

Wenn x = -3, fällt Komponente A zusammen. Wenn x = 2, fällt Komponente B zusammen. Jeder Wert bewirkt den Zusammenbruch des Fehlers, was bedeutet, dass unser ursprüngliches System (x^2 + x, das wir fast vergessen hätten!) unseren Anforderungen entspricht:

• Wenn x = -3, kollabiert der Fehler und wir erhalten (-3)^2 + -3 = 6.
• Wenn x = 2, kollabiert der Fehler und wir bekommen 2^2 + 2 = 6.

Alles zusammenfügen

Ich habe mich schon lange gefragt, wozu das Faktorisieren eigentlich gut ist. In der Algebra-Klasse werden Gleichungen bequemerweise auf null gesetzt, und wir sind uns nicht sicher, warum. Hier ist, was in der realen Welt passiert:

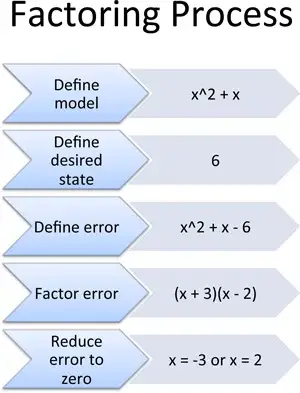
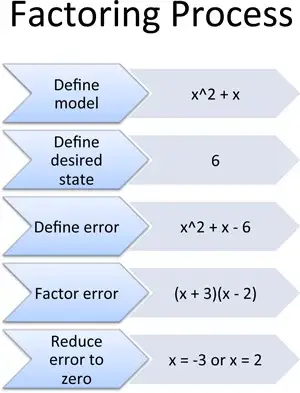
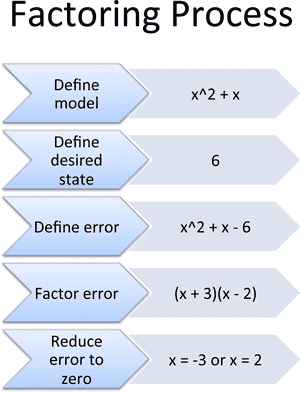
1. Definiere das Modell: Schreibe, wie sich dein System verhält (x^2 + x).
2. Definiere den gewünschten Zustand: Was sollte er sein? (6).
3. Definiere den Fehler: Der Fehler ist sein eigenes System: Fehler = tatsächlich – gewünscht (also x^2 + x – 6).
4. Faktorisiere den Fehler: Schreibe den Fehler als ineinandergreifende Komponenten um (x + 3)(x – 2).
5. Reduziere den Fehler auf null: Setze eine Komponente auf null oder die andere (x = -3 oder x = 2).

Wenn der Fehler = 0 ist, muss unser System den gewünschten Zustand erreicht haben. Wir sind fertig!

Algebra ist ziemlich nützlich:

• Unser System ist eine Trajektorie, der “gewünschte Zustand” ist das Ziel. Welche Trajektorie trifft das Ziel?
• Unser System sind unsere Verkäufe von Widgets, der “gewünschte Zustand” ist unser Umsatzziel. Welche Gewinnsumme erreicht das Ziel?
• Unser System ist die Wahrscheinlichkeit, unser Spiel zu gewinnen, der “gewünschte Zustand” ist ein 50-50 (fares) Ergebnis. Welche Einstellungen machen ein faires Spiel daraus?

Die Idee, ein System an seinen gewünschten Zustand anzupassen, ist nur eine Interpretation dafür, warum das Faktorisieren nützlich ist. Wenn ihr weitere Ideen habt, würde ich sie gerne hören!

Anhang

Eine Merkhilfe für den Vorgang:

Noch mehr zum Nachdenken:

• Multiplikation wird oft als UND betrachtet. Komponente A muss da sein UND Komponente B muss da sein. Wenn eine der Bedingungen falsch ist, bricht das System zusammen.
• Der Fundamentalsatz der Algebra beweist, dass man so viele “Komponenten” hat wie das höchste Polynom. Wenn der höchste Term x^4 ist, kannst du in 4 ineinandergreifende Komponenten faktorisieren (eine Diskussion für einen anderen Tag). Aber das sollte Sinn ergeben: Wenn du ein “x^4-System” in Multiplikationen umschreibst, sollten nicht 4 einzelne “x-Komponenten” multipliziert werden? Wenn es 3 wären, könntest du nie zu x^4 gelangen, und wenn es 5 wären, würdest du überschießen und einen x^5-Term bekommen.
• Hast du ein reales System in einer “Tipi”-Anordnung, bei dem ein einzelnes fehlerhaftes Bauteil die gesamte Struktur zum Zusammenbrechen bringt?
• Die quadratische Formel kann jedes System mit x^2-, x- und konstanten Komponenten “automatisch brechen”. Es gibt Formeln für komplexe Systeme (mit x^3, x^4 oder sogar einigen x^5-Komponenten), aber sie werden etwas verrückt.
• Gibt es einen Weg, ein System davon abzuhalten, diese Schwachpunkte zu haben? (Unfaktorisierbar? Nicht auf null setzbar?). Vergesst nicht, dass wir dachten, dass Systeme wie x^2 + 1 “nicht auf null setzbar” sind, bis die imaginären Zahlen auftauchten.

Viel Spaß mit Mathe!

Weitere Beiträge dieser Serie

1. Verständnis der Algebra: Warum faktorisieren wir Gleichungen?
2. Eine schnelle Intuition für parametrische Gleichungen
3. Intuition für die quadratische Formel
4. Intuition für die Punktsteigungsform
5. Intuition für graphische Funktionen
6. Intuition für Polynome