Bei der Auswertung von Marktforschungsdaten ist es üblich, signifikante Unterschiede zwischen verschiedenen Gruppen hervorzuheben. Es ist jedoch interessant zu beobachten, dass manchmal ein Unterschied zwischen zwei Gruppen als signifikant eingestuft wird, während ein größerer Unterschied zwischen zwei anderen Gruppen nicht als signifikant betrachtet wird. Ein möglicher Grund dafür könnte sein, dass die ersten beiden Gruppen größer sind als die anderen beiden.
Was ist ein Signifikanztest?
Ein beobachteter Effekt in einer Stichprobe, wie zum Beispiel der Unterschied zwischen zwei Gruppen, ist signifikant, wenn die Wahrscheinlichkeit gering ist, dass dieser Effekt zufällig aufgetreten ist. Wenn die Wahrscheinlichkeit p kleiner als ein vorgegebenes Signifikanzniveau a (normalerweise a = 0,05) ist, wird die Hypothese abgelehnt und der Effekt gilt als signifikant.
Abhängigkeit des Signifikanzniveaus vom Stichprobenumfang
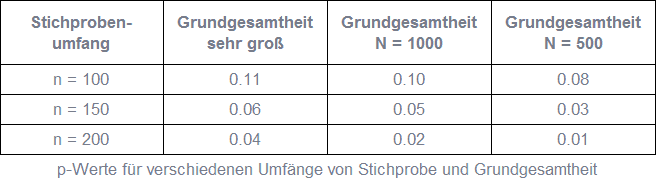
Angenommen, wir möchten überprüfen, ob das Ausprobieren eines Produkts einen positiven Einfluss auf die Kaufbereitschaft hat. Dazu nehmen wir bei zufällig ausgewählten Teilnehmern eine Bewertung der Kaufbereitschaft vor und nach dem Ausprobieren auf einer Skala von sieben Punkten vor. In unserer Stichprobe ergibt sich beispielsweise eine durchschnittliche Steigerung der Kaufbereitschaft um 0,2 Punkte nach dem Ausprobieren. Ist dieser Anstieg signifikant? Um diese Frage zu beantworten, testen wir die Einseitige Hypothese, dass die Kaufbereitschaft nach dem Ausprobieren nicht steigt. Die Tabelle zeigt die resultierenden p-Werte für verschiedene Stichprobenumfänge und Grundgesamtheiten. Obwohl der Mittelwert und die Standardabweichung in allen Fällen gleich sind, unterscheiden sich die p-Werte. Für eine große Grundgesamtheit ist die Steigerung der Kaufbereitschaft bei n = 100 und n = 150 nicht signifikant, da p größer als 0,05 ist. Bei n = 200 ist sie jedoch signifikant.
Mit anderen Worten, bei größeren Stichproben ist es wahrscheinlicher, dass eine Hypothese abgelehnt wird und ein Effekt als signifikant betrachtet wird, im Vergleich zu kleineren Stichproben. Das Verwerfen einer Hypothese bei einer kleinen Stichprobe deutet also auf einen stärkeren Effekt in der Grundgesamtheit hin als bei einer großen Stichprobe.
Statistischer Hintergrund
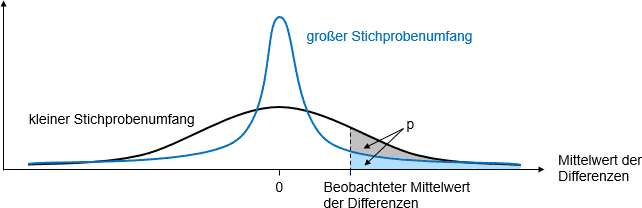
Ob ein Effekt signifikant ist oder nicht, hängt sowohl von den Ergebnissen in der Stichprobe als auch von der Stichprobenverteilung ab. Die Stichprobenverteilung beschreibt beispielsweise die Verteilung der Mittelwerte für alle möglichen Stichproben eines bestimmten Umfangs. In der Abbildung sind die Stichprobenverteilungen für zwei verschiedene Stichprobenumfänge dargestellt. Bei einem größeren Stichprobenumfang ist die Verteilung schmaler, was bedeutet, dass die Standardabweichung des Mittelwerts – der Standardfehler – kleiner ist. Die hellblaue Fläche unter der Kurve entspricht dem p-Wert für den größeren Stichprobenumfang. Bei einem kleineren Stichprobenumfang ist der p-Wert trotz des gleichen Ergebnisses in der Stichprobe aufgrund des größeren Standardfehlers größer.
Konsequenzen für gewichtete Daten
Eine Gewichtung der Fälle verändert nicht nur das Ergebnis in der Stichprobe, sondern hat auch Auswirkungen auf den Signifikanztest. Um sicherzustellen, dass die Signifikanz eines Effekts nicht fälschlicherweise begünstigt wird, sollte vermieden werden, dass die Summe der Gewichte größer als der ursprüngliche Stichprobenumfang ist. Stattdessen wird empfohlen, einen reduzierten Stichprobenumfang – die sogenannte “effektive Basis” – anzunehmen, die umso kleiner ist, je größer die Varianz der Fallgewichte ist.
Kleine Grundgesamtheiten und Vollerhebungen
In Fällen, in denen die Grundgesamtheit relativ klein ist, wie es bei B2B-Umfragen häufig der Fall ist, deckt die Stichprobe bereits einen großen Teil der Grundgesamtheit ab. Je größer das Verhältnis zwischen Stichprobenumfang und Größe der Grundgesamtheit ist, desto kleiner ist der Standardfehler. Das bedeutet, dass die Stichprobenverteilung schmaler wird und der p-Wert kleiner wird. Der Vergleich der p-Werte in der Tabelle für einen bestimmten Stichprobenumfang und verschiedene Grundgesamtheiten verdeutlicht diesen Zusammenhang.
Bei einer Vollerhebung können die tatsächlichen Werte der Grundgesamtheit bestimmt werden. Das Formulieren von Hypothesen über die Werte in der Grundgesamtheit und Signifikanztests sind dann nicht erforderlich. In unserem Beispiel würde bereits die geringste positive Abweichung des Mittelwerts von null auf einen positiven Effekt des Ausprobierens auf die Kaufbereitschaft hinweisen. Signifikanztests sind dann nur sinnvoll, um zu überprüfen, ob ein beobachteter Effekt aufgrund von Messfehlern zustande gekommen ist.
Dieser Beitrag basiert auf einem Artikel aus der Zeitschrift “planung&analyse”. Die Autoren Johannes Lüken und Prof. Dr. Heiko Schimmelpfennig sind erfahrene Experten auf dem Gebiet der Statistik und Marktforschung.
Literatur:
- Behnke, J.: Lassen sich Signifikanztests auf Vollerhebungen anwenden? Einige essayistische Anmerkungen. In: Politische Vierteljahresschrift, Jg. 46/2005, Heft 1, S. O-1-O-15.
- Kish, L.: Survey Sampling, New York et al., 1965, S. 427.
- Lipovetzky, S.: Post-Stratification with Optimized Effective Base. In: Proceedings of the Survey Research Methods Section, American Statistical Association, 2007, S. 2313-2320.